直方体の対角線

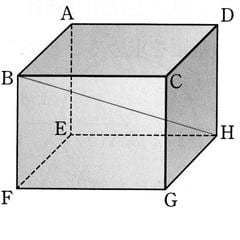
　三平方の定理の単元で直方体の対角線を求める授業をした。図の直方体ABCD－EFGHでBGの長さを求める。 AB=2cm, BC=4cm, BF=3cmである。
　まずはBGという対角線を見取り図で想像してもらう。つぎに段ボールで作った模型を提示する。 

　次に段ボールで作った模型を見せた。

　段ボールで作った模型は以前に記事にしたことがある。

　教科書では直角三角形BFHを見出し、三平方の定理を使っていたが、今回は長方形BFHDを導入した。長方形BFHDは直方体を真上から切った切り口になるので分かりやすいと思ったからだ。この長方形BFHD上に対角線BFが含まれている。

　模型で示してみた。

　こうすれば、対角線BHは長方形の対角線として求められる。
すなわち、
三角形BFHで
　BH²=FH²+BF²=FH²+3²

つぎに三角形HFGで
FH²=FG²+HG²=4²+2²

したがって、
BH²=（4²+2²）+3²=29

こうしてBHの長さはルート２９と求まったが、長方形BFHDの対角線になっているという考え方の方が分かりやすいと思うのだが、いかがだろうか？