中学校教科書にある確率３

ということで、一体何回サイコロを投げると相対度数が0.166や0.167に落ち着くのかが知りたくなってきた。計算回数を60000回にしてみた。
２０年前だと、１時間くらいかかったか・・・。PC9801でクロックスピードが16MHzだったかな。もう夕方だと遅くなるので、朝一でパソコンを起動して、プログラムを動かし、
朝の会に出てから、授業を終えてパソコンの前に・・・。計算結果がプリントアウトされていた。ここらあたりの計算時間は確かノートにとってあったのだが、探してみることにする。

今のパソコンでの60000回の結果。１回の計算は１秒ちょっとかかった。






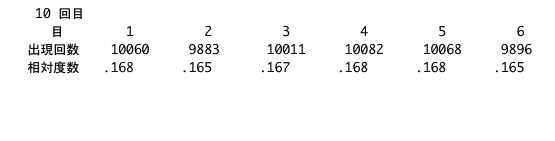
全然収束せずにバラバラの結果になる。

　そこで、確率統計の本を引っ張り出して、理論値の計算をしてみたところ、
90％の割合で0.166や0.167に収束するためには、４1万回以上の試行が必要だと分かった。４１万回以上のある回数をnとする。n≧410000
つまり、「n 回サイコロを投げ、相対度数を調べる」という実験をする。１０回に１回は0.166や0.167とは違った数が出ることも分かった。
「n 回サイコロを投げ、相対度数を調べる」実験を何ども繰り返すと、１０回に１回は0.166や0.167とは違った数が出るということである。
どうも、ここらの計算は自分でも自信がもてない。間違っているかもしれないが、あえてアップをした。

　後日、計算方法をアップするつもり。
　４１万回以上の根拠は・・・。
　２項分布で独立試行の数が大きくなるとほぼ正規分布に従うようになるので、正規分布表を利用して４１万回以上という数を得た。
正規分布表で相対度数が0.166以上0.167以下になる範囲の確率が0.9になるためのnの値を調べたのだ。（時間があれば後日アップ予定）

パソコンでは試行数が大きいと桁あふれになって計算不能になった。組み合わせの数　nCr を計算するときに、階乗のところで桁あふれが起こる。プログラムを工夫すればなんとかなるかも。