∠APB=(360度-∠AOB)÷2
したがって一定になる。
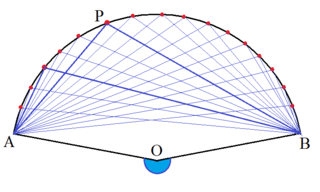
じつはこれは円周角の定理で中心角(青色角)が180度より大きい場合に当てはまっている。
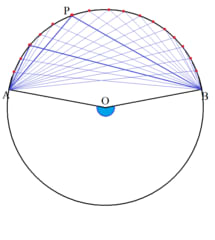
こうしてターレスの定理を一般化することによって円周角の定理が得られたわけである。
中心角が180度より小さい場合は次のような図になる。

前と同様にOPを結べば、

二つの二等辺三角形ができて、へこんだ四角形APBOの内角の和は
二つの三角形AOPと三角形BOPの内角の和だからやはり360度になる。
同様な論議で
∠APB=(360度-∠AOB)÷2
ただし∠AOBは上側の180度より大きいほうの角をいう。
360度-∠AOBは図の青色の角になる。
下の図で∠APB=(青色の角)÷2 が言える。

つづく

















