２次無理数の連分数展開

地蔵菩薩さんの選択用のテキストの中(P.34)に「ルート２」を連分数に展開したものが紹介されていた。UBASICというプログラム作成ソフトの付録に"confra.ub"というファイルネームで入っていた。’９４年にこのプログラムをUBASICで動かしていろいろな平方根の性質を調べたことがある。今日はこのプログラムを十進Basicに移植することが出来た。これでまた選択の授業がうまくやれそうだ。

地蔵菩薩さんのテキストから


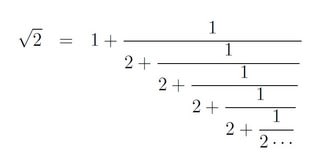
ルート２だと１＋のあとに２＋がずっと続くのでこのプログラムを動かすと、結果が １［２］ のように出力される
これは１＋のあと２＋　２＋　２＋　となることを表す。
ルート３だと１＋のあと１＋　２＋　１＋　２＋　が繰り返されるので、これが
１［１　２］と出力されます。どうして連分数で書けるのかは地蔵菩薩さんのテキストP.33を読んでみて下さい。連分数なんて知らなかった人は不思議な気分になりますよ。よかったらルート３を連分数に展開してみて下さい。（解答は後日）
　無理数（循環しない無限小数）であると習ったルート２やルート３が「連分数」という視点から眺めると、「循環連分数」というものだと分かります。
　おまけですが、このプログラムを動かして出力すると平方根は以下のようになります。

ルート５＝２［４］　　　　　　　循環節１
ルート６＝２［２　４］　　　　　循環節２
ルート７＝２［１　１　１　４］　循環節４
ルート８＝２［１　４］　　　　　循環節２
ルート１０＝３［６］　　　　　　循環節１

ルート２が１［２］
ルート５が２［４］
ルート１０が３［６］です何か気づきませんか？
ルート１７が４［８］なんです。
一般には」どうなっているのでしょう。公式が得られます。

こうしてパソコンで調べると平方根と連分数のおもしろい関係が得られます。



このプログラムリストは次の通りです。「十進Basic」で試してみて下さい。



プログラムリスト


1 !
2 !
3 ! ２次無理数の連分数展開
4 !
5 !
6 ! filename confra.bas
7 !
8 !
9 !
10 !
20 !
30 !
40 !
50 !
100 !
110 INPUT PROMPT "ｎ＝":n
120 IF n=0 THEN STOP
130 LET qn=INT(SQR(n))
140 IF qn=SQR(n) THEN GOTO 500
150 PRINT qn;"[";
160 LET c=n-qn^2
170 LET a=qn
180 LET a1=a
190 LET c1=c
200 ! repeat
210 LET k=INT((qn+a)/c)
220 PRINT k;
230 LET a=c*k-a
240 LET c=INT((n-a^2)/c)
250 IF (a<>a1)OR(c<>c1) THEN GOTO 200
260 PRINT "]"
270 PRINT
280 GOTO 110
290 !
500 PRINT qn;"の２乗です。"
510 PRINT
520 GOTO 110



END

壊れた？

　私のブログのレイアウトがおかしくなった。gooのサーバーでファイルが壊れたのか？選んだテンプレート通りにならないのはなぜだろう。・・・と思ったら、いつの間にか直っていた？原因は何だ？レイアウトがくずれて、左にあるべきカレンダーが上の方に平たく出てしまっていたのだけど。こんな経験ありませんか？