学校は室内なのに、くしゃみが出る。鼻が花粉を感知したようだ。職員室では何でもないのに、教室に行くとくしゃみが出る。たぶん生徒たちの制服に付いていた花粉が教室に舞っているのだろうと思う。特に4階の1年生の廊下に行くと感知する。1年生は活発だからか・・・。暖かくしていればいいのだが、寒い廊下では感知する上に、寒さを感じくしゃみがでるようだ。それにしても人間の体は敏感だと思った。
昨夜、目がかゆく、鼻水、くしゃみに咳、喉の痛みに悩まされた。今日ついにマスクを買った。花粉がひどいらしい。くしゃみが出てしょうがない。コンビニに飛込んだ。
マスクは昔ながらのガーゼマスク。今はやりの立体マスクは大袈裟な感じで好きではない。
マスクをして、鼻にティッシュを詰めた。それで何とか落ち着いた。今夜、無事眠れるだろうか。
マスクは昔ながらのガーゼマスク。今はやりの立体マスクは大袈裟な感じで好きではない。
マスクをして、鼻にティッシュを詰めた。それで何とか落ち着いた。今夜、無事眠れるだろうか。
放送担当を長らく務めてきたが、ビデオで撮った映像がどんどんたまってくる。普段の放送で流そうと思っても、テープだと頭出しなどが大変だ。DVDにすれば頭出しも可能なので、撮りためた映像をDVDにすることを計画。昨日、やっと今年度の入学式のDVDを作ることができた。もちろんチャプターもつけて、頭出しが出きるようにした。DVテープからパソコンのハードディスクに落としたデーターはDVDにデータとして保存した。こうすれば、もとのDVテープも、ハードディスクのデータも消去できる。
やっと実現した。少しずつこの作業をすすめて行きたい。次は体育祭の映像を整理する予定だ。
やっと実現した。少しずつこの作業をすすめて行きたい。次は体育祭の映像を整理する予定だ。
動画をDVDに焼いているときに、動画のキャプチャに必要なIEEE1394ケーブルが必要だったので、パソコンから抜こうとした。ところが・・・抜いたのはハードディスクのUSBケーブルだった。もし、動画を処理しているハードディスクのケーブルだったら・・・。
いままでの動画はすべて壊れてしまったはず。幸いにも、動画を処理しているハードディスクではない方を抜いたらしい。
いや違う!動画のハードディスクだった。ただしアクセスランプがついてなかったと思う。
いずれにせよ、おかげで動画ファイルは無事だったが・・・。ケーブルを抜くときはパソコンが処理をしていないときに抜くのが原則。初歩中の初歩だった。あせりは禁物。幸いだった。助かった!

いままでの動画はすべて壊れてしまったはず。幸いにも、動画を処理しているハードディスクではない方を抜いたらしい。
いや違う!動画のハードディスクだった。ただしアクセスランプがついてなかったと思う。
いずれにせよ、おかげで動画ファイルは無事だったが・・・。ケーブルを抜くときはパソコンが処理をしていないときに抜くのが原則。初歩中の初歩だった。あせりは禁物。幸いだった。助かった!
正五角形を探求してみましょう。
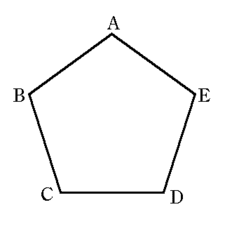
まずは、1辺の長さが与えられたとき、コンパスと定規を使って、正五角形を作図することから始めたいと思います。とりあえず1辺の長さを1とします。
作図するには、辺CDの垂直二等分線上に点Aがありますから、この点の位置を作図で求めれば良いわけです。

そのためにACの長さを求めます。AC=x とします。
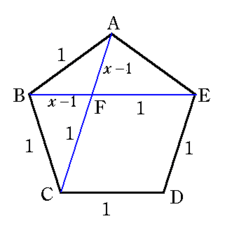
図のようにAC、BEを結び、その交点をFとします。
すると正五角形の性質から △BCA∽△FAB となります。
(理由:△BCAは二等辺三角形。頂角は正五角形の内角で108度。底角∠BAC=∠BCA=36度
△ABEでも同様に∠ABE=AEB=36度。したがって△FABで∠FAB=∠FBA=36度であるから、
△FABは二等辺三角形。底角がそれぞれ等しいので△BCA∽△FAB)
そのほか,△CBFと△EAFは合同な二等辺三角形ですから,図のように
BF=AF=x-1 となります。
BC:FA=CA:AB より
1:(x-1)=x:1
x(x-1)=1
x^2-x-1=0
これを解いて
x>0を考慮し
x=1/2(1+sqrt(5))
AC=1/2+sqrt(5)/2 であることが分かりました。
このACの長さををどうやって作図で求めるのかですが、
CDの垂直二等分線を引けばで1/2はつくることができます。
図のようにMN=CDとして,CDの中点Mから1の長さをとれば、
MN=1,CM=1/2 となり,
三平方の定理からCN=sqrt(5)/2 ですから、
あとはこのCNにCMを加えれば良いわけです。
(NF=CM=1/2)
CFがその長さとなり,CA=CFとなるように点Aをとります。
こうして、点Aが決まりました。

あとは、A, C,Dを中心として半径1 の円をかけば
交点B,E が得られます。
良かったら,正五角形を作図してみて下さい。
次は、半径1 の円に内接する正五角形を作図してみます。
(続く)

まずは、1辺の長さが与えられたとき、コンパスと定規を使って、正五角形を作図することから始めたいと思います。とりあえず1辺の長さを1とします。
作図するには、辺CDの垂直二等分線上に点Aがありますから、この点の位置を作図で求めれば良いわけです。

そのためにACの長さを求めます。AC=x とします。

図のようにAC、BEを結び、その交点をFとします。
すると正五角形の性質から △BCA∽△FAB となります。
(理由:△BCAは二等辺三角形。頂角は正五角形の内角で108度。底角∠BAC=∠BCA=36度
△ABEでも同様に∠ABE=AEB=36度。したがって△FABで∠FAB=∠FBA=36度であるから、
△FABは二等辺三角形。底角がそれぞれ等しいので△BCA∽△FAB)
そのほか,△CBFと△EAFは合同な二等辺三角形ですから,図のように
BF=AF=x-1 となります。
BC:FA=CA:AB より
1:(x-1)=x:1
x(x-1)=1
x^2-x-1=0
これを解いて
x>0を考慮し
x=1/2(1+sqrt(5))
AC=1/2+sqrt(5)/2 であることが分かりました。
このACの長さををどうやって作図で求めるのかですが、
CDの垂直二等分線を引けばで1/2はつくることができます。
図のようにMN=CDとして,CDの中点Mから1の長さをとれば、
MN=1,CM=1/2 となり,
三平方の定理からCN=sqrt(5)/2 ですから、
あとはこのCNにCMを加えれば良いわけです。
(NF=CM=1/2)
CFがその長さとなり,CA=CFとなるように点Aをとります。
こうして、点Aが決まりました。

あとは、A, C,Dを中心として半径1 の円をかけば
交点B,E が得られます。
良かったら,正五角形を作図してみて下さい。
次は、半径1 の円に内接する正五角形を作図してみます。
(続く)
昨日、もう一度4次方程式を解いたノートを見てみたところ、定数項の符号が反対だったことが分かった。早速計算し直して代入したらOK。つまり =0になった。なーんだと思われるかも知れないが、大変悩んだ。
解いてみた4次方程式は
x^5-1=0 を解くとき因数分解し
(x-1)(x^4+x^3+x^2+x+1)=0
x-1=0 の残り x^4+x^3+x^2+x+1=0
すでにこの解は分かっている。円周等分方程式の解だから
正五角形をかいて求めてもよいし、三角関数を使って解いても良い。
結果は図を使って求めていたのだが、実際に4次方程式を解いてみたかった。
30年以上も数学の教師をしていたのだが、中学生を教えていたので、こんな4次方程式を解く必要がなかったから、やっていなかった。不勉強を恥じる。
解は二重根号で表されるためにここの画面では表現しづらい。正五角形の図も含めて
「はてな」のブログで紹介したと思っている。準備ができたら後日アップします。
解いてみた4次方程式は
x^5-1=0 を解くとき因数分解し
(x-1)(x^4+x^3+x^2+x+1)=0
x-1=0 の残り x^4+x^3+x^2+x+1=0
すでにこの解は分かっている。円周等分方程式の解だから
正五角形をかいて求めてもよいし、三角関数を使って解いても良い。
結果は図を使って求めていたのだが、実際に4次方程式を解いてみたかった。
30年以上も数学の教師をしていたのだが、中学生を教えていたので、こんな4次方程式を解く必要がなかったから、やっていなかった。不勉強を恥じる。
解は二重根号で表されるためにここの画面では表現しづらい。正五角形の図も含めて
「はてな」のブログで紹介したと思っている。準備ができたら後日アップします。
文化祭の合唱コンクールの動画をパソコンに落としてみた。何か動きがぎこちないと思ったが、まあいいやと思ってDVDに焼いてみた。DVDを動かしてみた動画はとても見られたものではなかった・・・
wmなんとかという拡張子がついているやつ。Win XP付属のムービーメーカーでパソコンに取り込んだが、画質が悪すぎた。念のためにファイルサイズを確認したら、異常に小さかった。
というわけで、Win付属のソフトはあまり役には立たないことが分かった。やはりmp2かaviファイルでないと画質の良いものは得られない。残念、せっかく取り込んだというのに・・・。

wmなんとかという拡張子がついているやつ。Win XP付属のムービーメーカーでパソコンに取り込んだが、画質が悪すぎた。念のためにファイルサイズを確認したら、異常に小さかった。
というわけで、Win付属のソフトはあまり役には立たないことが分かった。やはりmp2かaviファイルでないと画質の良いものは得られない。残念、せっかく取り込んだというのに・・・。

ヒルベルトの幾何学基礎論を読んでいるところ。難解。「これかー」と思った。つまり「点、直線、平面とは何か」などが書かれているのではない。ものの集まりとして点、直線、平面を扱っている。こんなの確か学生時代に紹介されていた記憶があったなー、と思った。
公理が多い!もっと少ないと思っていたのに・・・。これはとても読み切れるものでもないし、理解もできないと思った。読み飛ばしに限る。
これを読めば、「公理」に関する感覚が身に付くだろうと思う。その感覚を利用して「特殊相対性理論」が理解できそうだが、しばらくは「積ん読」か。
公理が多い!もっと少ないと思っていたのに・・・。これはとても読み切れるものでもないし、理解もできないと思った。読み飛ばしに限る。
これを読めば、「公理」に関する感覚が身に付くだろうと思う。その感覚を利用して「特殊相対性理論」が理解できそうだが、しばらくは「積ん読」か。
3年生のラスト授業のついでに
5次方程式 x^5-1=0 について考えてみた
(x-1)(x^4+x^3+x^2+x+1)=0
と因数分解できるから
x^4+x^3+x^2+x+1=0 を解いてみようと思った。
円に内接する正五角形の作図で、この方程式の解は分かっているのだが
フェラーリの方法で解いてみた。
いろいろやって、うまくいったと思ったのだが・・・。
検算するとうまくいかない。4次方程式恐るべし。
うまくいったらアップします。
5次方程式 x^5-1=0 について考えてみた
(x-1)(x^4+x^3+x^2+x+1)=0
と因数分解できるから
x^4+x^3+x^2+x+1=0 を解いてみようと思った。
円に内接する正五角形の作図で、この方程式の解は分かっているのだが
フェラーリの方法で解いてみた。
いろいろやって、うまくいったと思ったのだが・・・。
検算するとうまくいかない。4次方程式恐るべし。
うまくいったらアップします。

x^2+x+1=0 を解く
1を右辺に移項
x^2+x=-1
両辺に1/2の2乗を加える
x^2+x+(1/2)^2=-1+(1/2)^2
因数分解と計算をする
(x+1/2)^2=-3/4
( )^2=(負の数)
2乗したら負の数になる数、つまり負の数の平方根はない、と中学校では
学んだ。
小学校では「0より小さい数はない」と習ったが、中学校では「ある」と習ったように
中学校では「負の数の平方根はない」と習ったけれども(教えたけれども)、高校では
「ある」と習う。
で、実はある。高校ではこのような数を「虚数」と習う。
x+1/2=±sqrt(-3/4)=±sqrt(-3)/2
と、負の数の平方根を求めしまう。
x=-1/2±sqrt(-3)/2=(-1±sqrt(-3))/2
ここでsqrt(-1)を「虚数単位」といい文字iで表す。
ある数を文字で表すのは円周率π があるが、それと同じように iで表す数がある。
このあと1+3i の様な数を座標平面の(1, 3)で表すことを紹介。
最後にx^3-1=0の3つの解が座標平面で正三角形3つの頂点のように並ぶことを紹介して、授業を終えた。
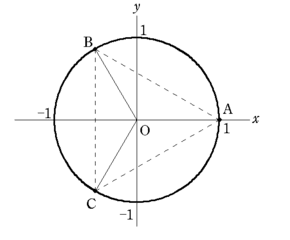
点Aは 1
点Bは (-1+sqrt(3)i)/2
点Cは (-1-sqrt(3)i)/2
もし次にこういう機会があったら、方程式x^5-1=0 の解を紹介して
解を表す点がが正五角形の頂点に並ぶことを示してみたい。
1を右辺に移項
x^2+x=-1
両辺に1/2の2乗を加える
x^2+x+(1/2)^2=-1+(1/2)^2
因数分解と計算をする
(x+1/2)^2=-3/4
( )^2=(負の数)
2乗したら負の数になる数、つまり負の数の平方根はない、と中学校では
学んだ。
小学校では「0より小さい数はない」と習ったが、中学校では「ある」と習ったように
中学校では「負の数の平方根はない」と習ったけれども(教えたけれども)、高校では
「ある」と習う。
で、実はある。高校ではこのような数を「虚数」と習う。
x+1/2=±sqrt(-3/4)=±sqrt(-3)/2
と、負の数の平方根を求めしまう。
x=-1/2±sqrt(-3)/2=(-1±sqrt(-3))/2
ここでsqrt(-1)を「虚数単位」といい文字iで表す。
ある数を文字で表すのは円周率π があるが、それと同じように iで表す数がある。
このあと1+3i の様な数を座標平面の(1, 3)で表すことを紹介。
最後にx^3-1=0の3つの解が座標平面で正三角形3つの頂点のように並ぶことを紹介して、授業を終えた。

点Aは 1
点Bは (-1+sqrt(3)i)/2
点Cは (-1-sqrt(3)i)/2
もし次にこういう機会があったら、方程式x^5-1=0 の解を紹介して
解を表す点がが正五角形の頂点に並ぶことを示してみたい。

















