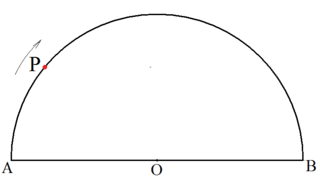
「ターレスはここであることに気がついた」とかなんとかできたら良いのだが、ここではまだ あがっていたから
いきなり「∠APBの大きさは何度でしょうか?」と問いかけた。
生徒の方から「90度」という声がした。
「そうかな?では調べてみよう」と言って、三角定規の直角の所を示して。
「90度はここの角度だから、合わせてみるといいね」
といって、直角のところを∠APB合わせてみると、ピッタリ合う。
「どうやら90度のようだね」
「ではその理由を考えてみよう。本当にこの角が90度であることを説明、つまり証明してみよう。」
「どうやったら90度であることを証明出来ますか?」
意見が出ないときは
「このままでは証明出来ないね。この図中途半端だね、何かやりたいね」という。
ここでは「PとOを結ぶ」と答えてくれた。
・・・で、実際に結んでみると・・・。

「そうだね、これを手がかりにしてこの図から何か考えられないかな」
「2つ三角形が出来たね。これはどんな三角形だろう」
などと問いかけると
「二等辺三角形」という返事が返ってくる。
「二等辺三角形だとすると色々な性質がありそうだ」
「どうして二等辺三角形なのかな」という問いかけが大事。描いている図形が円であることを強調する。
「円だから」「Oは円の中心だから」とかいろいろ出てくる。
△OAPはOA=OP,△OBPはOB=OP ということを確認する。

二等辺三角形の底角は等しいから、図の青丸○と赤丸●の角は等しい。
もうひといき。
つづく