プログラミング造りで何某かの糧を得ている身としては腕が錆つくと非常に困る。
で思い出した様に今回作ったのがガウス・ジョルダン法による連立方程式の解を求めるプログラム。
DataGridViewとか配列計算とかいろいろと頭の訓練が必要で結構面白かった、が、使い道は全く無い。
でも材料費はセロ、接着材も塗料もいらないので費用は掛からない、ただ暇と根気だけが必要。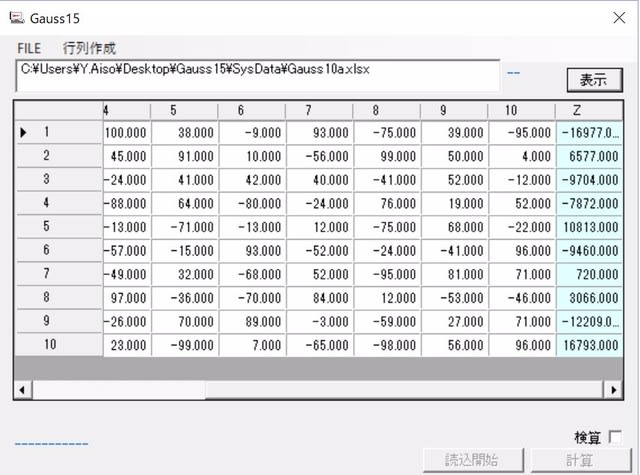
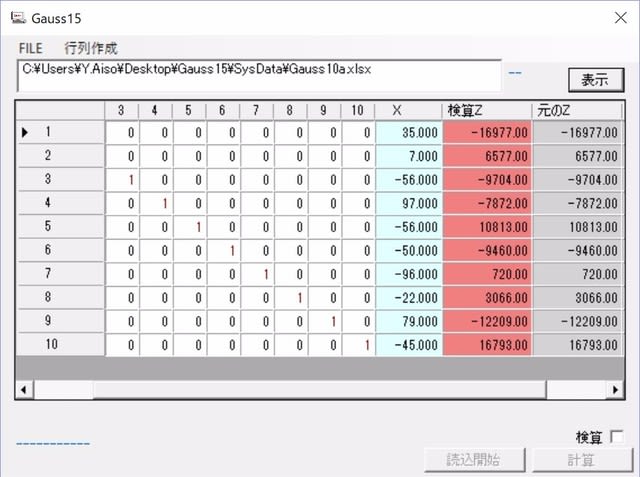
左側は自動生成した10行10列+1列の連立方程式、右側が求めたXと検算結果。
昨今のPCの性能だと「アッ!」という間に計算は終えるが、100×100位になると10秒以上は掛かる。
(500×500だと破綻無く動作し約6分掛かった、ここらへんがプログラムを造ると面白い所。)
昔は行列による連立方程式の解法は大嫌いで、試験で5×5位の問題が出た時には中学生方式で解いてさも行列で解いたかの様に見せかけて得点したことがあった。今じゃそれほどのアレルギーは無い。
一応このプログラムはエクセル表で入力してエクセル表で吐き出す様にしてあるから実用性はあり、でもくどい様だが残念ながら使い道は無い。
(ソースも連立方程式だけだとこの位:ピボット交換は省略)
For II = 0 To inCC - 2
'Normalize
DeW0 = deTAb(II, II)
For k = 0 To inCC - 1
deTAb(II, k) = deTAb(II, k) / DeW0
Next
'Each Rows
For Irow = 0 To inCC - 2
If Irow <> II Then
DeW0 = deTAb(Irow, II)
For KK = 0 To inCC - 1
deTAb(Irow, KK) = deTAb(Irow, KK) - DeW0 * deTAb(II, KK)
Next
End If
Next
Next II

















