横浜三渓園のヒガンバナです。
ずいぶん、朝夕過ごしやすくなってきました。
ようやく、神奈川県も「緊急事態宣言」が明けそうな感じです。
学校に活気が戻ってくるとよいです・・・
生活上は、気を付けることは変わりませんが。
突然ですが、問題です。
「２５０枚の色紙を、さゆりさんとまことさんの色紙の枚数の比が
３：２になるように分けます。
２人の色紙の枚数は、それぞれ何枚ですか。」
・・・６年生の算数の教科書の問題です。
３と２と２５０はどういう関係になっているのか？
比の部分を定規で線を引いて表します。
比「１」につき「１ｃｍ」。
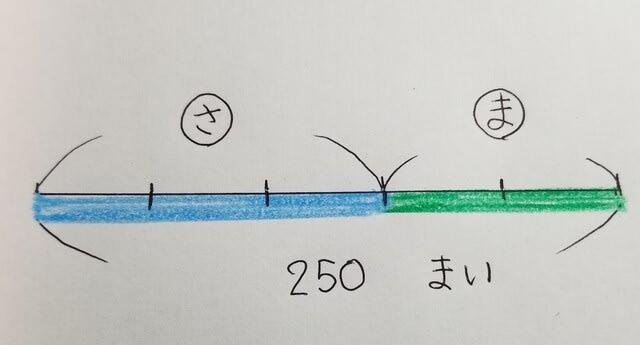
「さ」はさゆりさん、「ま」はまことさん。全体が２５０枚。
５つに分けた「１つ分」が分かれば、それぞれがわかります。
さゆりさんは、３つ分、まことさんは、2つ分。
教科書にも線分図がのっています。
でも、「図」って自分で描いたほうがより分かりやすい。
比１つ分を１ｃｍにかけば、この「手」の問題は、パターンが違っても
自分で図が描けます。（
と定規があれば！）「文章」からだけだと、「イメージ」がわきにくい子も
そんなに練習しなくてもすぐ解けます！
算数の応用問題は、イラストや図がついてくることも多いのですが
自分に「合った」図でないとかえってわかりにくくなることも。
教科書では、さらに
「比の値」や「等しい比」を使った方法がのっています。
最近思うのは、
「自分に合った方法でなおかつ、ほとんどのパターンで使える方法」
を見つけることが文章題や計算の早道なのでは・・・ということです。
もちろん、いろいろな解法を知っておくことは
数学的な力を高めます。
でも、とりあえずいつでも使える「ホームベース」っぽいものがあるって
安心ですよね💛
ずっと昔ブログに書いたような気がするのですが、
定規で「九九」もできます。
６の段を忘れてしまったら・・・・
０の目盛りから６ミリずつ目盛りをつけていくと
６，１２（１ｃｍ２ｍｍ）、１８（１ｃｍ８ｍｍ）・・・・
この方法は、何度九九を唱えても覚えられない２年生の子が発明しました！
まさに「必要は発明の母」
みんなと違っても「不正でなく」「手軽に」「何度も」使える方法・・・・
算数だけでなく、いろんな学習に使えそうです。
私は最近、自分が「暗記」するとき、視線を動かすのが「横」でなく「縦」向きでした方がよいことに
自分で気づきました！
大人になっても「進化」していきたいです。
）
個別学習塾びすぽうくのホームページへ
（色のついているところをクリックしてください）
していたのが、
）
（色のついているところをクリックしてください）
