『リスパの法則』『リスク』『リターン』

🌸リスパの法則を理解する

⛳ゲーム４－２
　☆ゲームＡでは

　＊１の目が出ると１００円を支払い、６の目が出ると１００円もらえる
　☆ゲームＢでは

　＊１の目が出ると１００0円支払い、６の目が出ると１０００円もらえる

　＊手元に１０００円のお金があるとして、どちらのゲームが有利か？
　☆「リスク」という言葉は、ふつうは「危険」のことをいいう
　☆統計学でいうリスクは

　＊「儲かる可能性と損する可能性のばらつき」のこと
　☆ゲームＡも、ゲームＢも

　＊サイコロを振って１の目が出るとお金を払い

　＊６の目が出るとお金がもらえます

　＊１か６が出る確率は、どちらも６分の１で同じ
　☆ゲームＡ

　＊勝つ（６の目）で100円もらえ、負ける(１の目）と１００円払う
　☆ゲームＢ

　＊勝つと１０００円もらえますが、負けると１０００円払う

　☆期待値は、ゲームＡでもゲームＢでもゼロ円
　＊ゲームＡを「リスクが小さい」、ゲームＢを「リスクが大きい」という
　☆リスクが小さいゲームＡ

　＊負けても１００円の損、勝っても１００円の得
　☆リスクが大きなゲームＢ

　＊負けると１０００円払い、勝つと１０００円儲かる
　＊リスクの大きさは三角形の底辺で表わせる

⛳勝ったときのことよりも、最悪のことが起きたときのことを考える
　☆ゲームＡとゲームＢは、リターン（期待値）がどちらもゼロ円

　＊リスクの大きさだけがちがう

　＊どちらかのゲームにチヤレンジしなければならないのか
　☆期待値がゼロ円ということは

　＊ゲームを何度も繰り返すと、勝ち負けの合計はゼロに近づいていく
　＊どちらを選んでもいっしょのように思えるが

　☆「リスクの小さなゲームを選んだほうがいい」が正解

⛳最悪のことが起きたときのことを考える

　☆運がよくて、２回続けて６が出るケースもある

　＊３６回に１回くらい起こる
　＊もらえるお金は、ゲームＡだと２００円、ゲームＢだと２０００円

　＊ゲームＢが圧倒的に有利に見えますが、合計は期待値のゼロに近ずく
　（これが大数の法則でした）
　☆運が悪くて２回続けて１が出るケースもある
　＊３６回に１回くらい起こる
　☆手持ちの資金は１０００円なので

　①ゲームＡだと、２００円を払ってもまだ８００円残る
　＊勝ち負けの合計はいずれ期待値に近づいていく

　＊ここから挽回することも十分可能です
　➁ゲームBだと、最初に１が出たときに１０００円を払うので

　＊手持ちのお金がなくなってしまいます

　＊次に１が出ると、もう払うお金はないのですから、ゲームオーバー

⛳リスパ（リスクパフォーマンス）の法則

　☆人生というゲームはずっと続く

　＊ゲームオーバーになるようなリスクをおかしてはいけない
　☆リスパの法則①

　＊「期待値が同じなら、リスクが小さいほうを選べ」

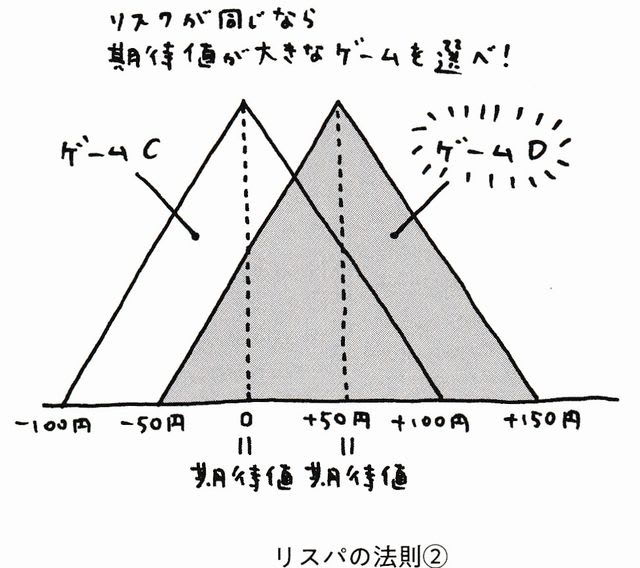
　☆リスパの法則②

　＊「リスクが同じなら、期待値が大きなほうを選べ」

　＊ゲームＣよリゲームＤを選ぶのがリスパの法則

　　　　　　　　　　　　　　　　　　　　　　（敬称略）
⛳知識の向上目指し、記事を参考に自分のノートとしてブログに記載
⛳出典内容の共有、出典の購読、視聴に繋がればと思いブログで紹介
　☆記事内容ご指摘あれば、訂正・削除します
⛳私の知識不足の為、記述に誤り不明点あると思います
⛳投資は、自己責任、自己満足、自己判断で
⛳詳細は、出典原書・記事・番組・画像でご確認ください
⛳出典、『どうしたらお金持ちになれるの？』

『リスパの法則』『リスク』『リターン』

（『どうしたらお金持ちになれるの』記事他より記事画像引用）

『投機』『投資』『ヘタな投資の罪』

🌸投資という名の「転売」２

　☆経済等の根本を語っているのである面で納得しますね

　☆しかし、ある面では、現在の経済との整合性、活用に？

⛳資産価格の上昇と「コロナ禍マスク問題」の共通点
　☆不動産もまた、投資や投機の対象になる

　＊東京の新築マンションの坪単価

　＊１０年で４０％近く上がっている

　＊「資産価格が上がった」と喜んでいる人も多い

　☆資産価格の上昇で、効用は増えているのではない
　＊これもまた、先ほどの株価と同じだ

　☆交通網が発達したり町が発展したりすることで利便性が高まり

　＊結果マンションの価格が上がっているのであれば喜ばしいことだ

　☆この１０年で東京の利便性が４０％も増えたか

　＊利便性と不釣り合いに価格が上がったように感じる

　☆資産価格が上がって喜べるのは

　＊「自分が使っていないもの」を転売目的で保有している人たちだ

　＊投機をする人は、自分が住まないマンションを買う
　＊自分が使わないものを持つことで、誰かが使えなくなっているのだ

　☆コロナ禍でのマスクの転売問題と本質的に同じだ
　＊新型コロナウイルスが流行し始めたとき

　＊マスクが手に入らないという事態が日本全国で起きた

　＊転売目的で大量のマスクを買い占める人が出てマスクの価格は高騰

　＊通常の１００倍以上の価格で取引された例もあった

　＊高騰によって、彼らが大量に保有するマスクの資産価格は増えたが

　＊多くの人がマスクを使えず、多くの人から効用を奪ったのだ
　＊被害者の存在も加害者の存在もはっきりわかるし

　＊その因果関係もわかりやすいから

　＊転売する人たちが悪さをしていることが明るみに出た
　☆マンションの転売も、本質的には同じことだ

　＊自分が使わないものを買っておいて、本当に使いたい人に高く売る

　☆投機と言うギャンブルをするぐらいなら

　＊そのお金を銀行に眠らせておいたほうがまだいい

　☆「銀行にお金を眠らせているのはもったいない」というアドバィス

　＊かなり無責任なセリフだ

⛳投資とは「将来のために使う労力」だ
　☆僕たちはいろんな場面で投資という言葉を使う
　＊「将来の為にお金や労力を使う」という共通点がある
　☆勉強が投資と呼ばれるのは

　＊自分の将来の可能性を広げることに労力を使うからだ
　☆公共投資によつて道路や図書館が作られるのは

　＊将来の人々の暮らしを良くするためだ
　☆会社へ投資されたお金は

　＊その会社が提供する将来の商品の生産準備や研究開発に使われる
　☆投資されたお金は事業主を通して流れ

　＊多くの労働がつながり、事業を始めることができる

　＊そして、その事業の成功が、僕たちの将来の生活を豊かにする

　＊新たなモノやサービスを利用できるようになる

⛳投資とギャンブルの違い
　☆多くの人が想像する投資は

　＊投機と呼ばれるギャンブルであることが多い
　☆本当の意味で投資されたお金は

　＊多くの人に働いてもらうことに使われる

　＊その人たちが働くことで、新たな価値を生み出すことができる

　☆お金を奪い合うギャンブルとは真逆の、生産的な活動だ

⛳ヘタな投資の罪
　☆投機だろうと投資だろうと、誰もが儲けたいと思っている

　☆しかし、投機と投資では「損」の意味が違う
　☆ヘタな投機はただの恥だが、 ヘタな投資は大いなる罪だ
　＊投機はお金の奪い合いだから

　＊誰かが損をしても反対側で誰かが儲けている

　＊損はあくまでも個人の問題であって

　＊社会から何かが失われるわけではない
　☆投資で損をしても、お金が消えるわけではない

　＊その事業のために働いてくれた人々に流れるだけで

　＊全体のお金の量は変わらない

　☆投資で損をする場合

　＊その事業に費やされた労働に対して

　＊お客さんが感じた効用が少なすぎるということ

　　　　　　　　　　　　　　　　　　　　　　　　　　（敬称略）
⛳知識の向上目指し、記事を参考に自分のノートとしてブログに記載
⛳出典内容の共有、出典の購読、視聴に繋がればと思いブログで紹介
　☆記事内容ご指摘あれば、訂正・削除します
⛳私の知識不足の為、記述に誤り不明点あると思います
⛳投資は、自己責任、自己満足、自己判断で
⛳詳細は、出典原書・記事・番組・画像でご確認ください
⛳出典、『お金の向こうに人がいる 』

『投機』『投資』『ヘタな投資の罪』

（ネットより画像引用）

宮崎観光（宮崎⇒延岡⇒高千穂）３

🌸高千穂

　

　☆豊かな自然と神話の世界が融合した、神秘的で美しい場所

　☆雄大な自然

　＊高千穂峡の切り立った岩壁と五ヶ瀬川のコントラストは美しい

⛳高千穂峡

　☆神話の世界

　＊天岩戸隠れ神話で有名な天岩戸神社や、高千穂神社など

　＊古くからの神話が息づく場所が多い

　＊神秘的な雰囲気に包まれている

　☆高千穂峡

　＊貸しボートに乗って峡谷の底から見上げる景色は格別

⛳高千穂神社

　☆大きな夫婦杉が有名で、良縁祈願に訪れる人も多い

　☆高千穂神社 夫婦杉が有名

　☆国史見在社「高智保皇神」の有力な論社であるが

　＊近代社格制度上は村社にとどまった

　＊現在は神社本庁の別表神社となっている

⛳天岩戸神社

　☆日本神話で有名な天岩戸が祀られている神社

　☆あまりにひどいいたずらにお怒りになりました天照大御神様

　☆天岩戸と呼ばれる洞窟にお隠れになられた

⛳真名井の滝

　☆高千穂峡にある美しい滝

　☆マイナスイオンをたっぷり浴びることができる

⛳天安河原

　☆天地暗黒となり八百万の神がこの河原で対策を相談した

　　　　　　　　　　　　　　　　　　　　　　　（敬称略）
⛳知識の向上目指し、記事を参考に自分のノートとしてブログに記載
⛳出典内容の共有、出典の購読、視聴に繋がればと思いブログで紹介
　☆記事内容ご指摘あれば、訂正・削除します
⛳私の知識不足の為、記述に誤り不明点あると思います
⛳投資は、自己責任、自己満足、自己判断で
⛳詳細は、出典原書・記事・番組・画像でご確認ください
⛳出典、『Ｇｅｍｉｎｉ』、ネットより記事引用