14日に指された第10期女流王座戦五番勝負第五局。
振駒で里見香奈女流四冠の先手。先手の中飛車,後手の西山朋佳女流王座の三間飛車の相振飛車から角交換となり相向飛車に。後手がそれでいけるとみたのか苦戦とみて勝負をかけたのかは不明ですか,大きく駒損をする攻めを敢行。このために先手がリードを奪いましたが,受け切って勝つのか攻め合って勝つのかの判断が中途半端で,後手が盛り返すという展開に。

これは後手が1九の銀で香車を取った局面。先手は持駒が十分で,さらに3二の角も必ず取れる形なので,ここは急いで攻める必要はなく,☗6九香と打っておけばほぼ負けはありませんでした。しかしすぐに☗3二とと取ったために☖3九龍☗4七玉☖3七銀成☗同銀☖2七香成と攻められることに。
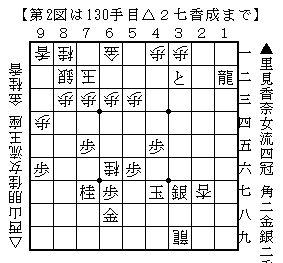
第2図から☗3一と☖4二香と王手をしてから☗4八銀と受けたのが最終的な敗着。合駒に打たせた香車が先手玉への攻めに働いたために,簡単に先手玉が寄ってしまいました。単に☗4八銀なら先手が残していました。
3勝2敗で西山王座が防衛。第9期からの連覇で2期目の女流王座です。
僕の結論としては,1675年にステノNicola Stenoが書簡六十七の二を書いたとき,『新科学対話Discorsi e dimostrazioni matematiche, intorno a due nuove scienze attenenti alla mecanica ed i movimenti locali』を意識してデカルトRené Descartesの哲学を新哲学といった可能性はきわめて低く,1638年にガリレイGalileo Galileiが『新科学対話』を出版したとき,デカルトの新哲学を意識して自身の科学を新しい科学といった可能性は否定できないということになります。とりわけ,『新科学対話』が出版されたのが,イタリアではなく,この時期にデカルトが活動していたオランダであったことも,この結論を補強する要素にはなり得るかもしれません。とはいえこれはあくまでも僕の見解opinioであって,史実がそうであったと主張したいわけではないという点は理解しておいてください。
この部分の考察は,新科学から新哲学へ向かう僕自身の連想,いい換えれば僕の精神mensのうちの表象像imaginesの結合に由来します。僕はこれを,スピノザが第二部定理一八の備考Scholiumで具体的な事例をあげているような表象像の結合といいます。新科学にせよ新哲学にせよ,それはあくまでもことばから別のことばへの連想なのであって,ことばというものが一般的に記号である以上,それは十全な観念idea adaequataから十全な観念への移行と解するべきではなく,混乱した観念idea inadaequataから混乱した観念への,つまり表象像から表象像への移行であると解するべきだからです。そしてこの表象像の移行あるいは表象像の結合は,僕自身の精神のうちで生じたことなのであって,河合自身がコラムの中で言及しているというわけではありません。なのでこれに関する探究はここまでとして,河合自身がコラムの中で言及している事柄を対象とした考察に移ることにします。
繰り返しになりますが,『新科学対話』というのは,ガリレイの分身と思しきサルヴィヤチSalvyachiという人物が,弟子の質問に解答するという形式で進められていきます。その中に,もしAとBという2本の線がある場合,線の中には無限に多くのinfinita点が含まれているがゆえに,もしも線Aの方が線Bよりも長いのであれば,線Aに含まれている点の無限infinitumの量は,線Bに含まれている点の無限の量よりも大きいという見解に対して,サルヴィヤチが答えている部分が含まれています。まず河合はこの部分に着目しています。
振駒で里見香奈女流四冠の先手。先手の中飛車,後手の西山朋佳女流王座の三間飛車の相振飛車から角交換となり相向飛車に。後手がそれでいけるとみたのか苦戦とみて勝負をかけたのかは不明ですか,大きく駒損をする攻めを敢行。このために先手がリードを奪いましたが,受け切って勝つのか攻め合って勝つのかの判断が中途半端で,後手が盛り返すという展開に。

これは後手が1九の銀で香車を取った局面。先手は持駒が十分で,さらに3二の角も必ず取れる形なので,ここは急いで攻める必要はなく,☗6九香と打っておけばほぼ負けはありませんでした。しかしすぐに☗3二とと取ったために☖3九龍☗4七玉☖3七銀成☗同銀☖2七香成と攻められることに。

第2図から☗3一と☖4二香と王手をしてから☗4八銀と受けたのが最終的な敗着。合駒に打たせた香車が先手玉への攻めに働いたために,簡単に先手玉が寄ってしまいました。単に☗4八銀なら先手が残していました。
3勝2敗で西山王座が防衛。第9期からの連覇で2期目の女流王座です。
僕の結論としては,1675年にステノNicola Stenoが書簡六十七の二を書いたとき,『新科学対話Discorsi e dimostrazioni matematiche, intorno a due nuove scienze attenenti alla mecanica ed i movimenti locali』を意識してデカルトRené Descartesの哲学を新哲学といった可能性はきわめて低く,1638年にガリレイGalileo Galileiが『新科学対話』を出版したとき,デカルトの新哲学を意識して自身の科学を新しい科学といった可能性は否定できないということになります。とりわけ,『新科学対話』が出版されたのが,イタリアではなく,この時期にデカルトが活動していたオランダであったことも,この結論を補強する要素にはなり得るかもしれません。とはいえこれはあくまでも僕の見解opinioであって,史実がそうであったと主張したいわけではないという点は理解しておいてください。
この部分の考察は,新科学から新哲学へ向かう僕自身の連想,いい換えれば僕の精神mensのうちの表象像imaginesの結合に由来します。僕はこれを,スピノザが第二部定理一八の備考Scholiumで具体的な事例をあげているような表象像の結合といいます。新科学にせよ新哲学にせよ,それはあくまでもことばから別のことばへの連想なのであって,ことばというものが一般的に記号である以上,それは十全な観念idea adaequataから十全な観念への移行と解するべきではなく,混乱した観念idea inadaequataから混乱した観念への,つまり表象像から表象像への移行であると解するべきだからです。そしてこの表象像の移行あるいは表象像の結合は,僕自身の精神のうちで生じたことなのであって,河合自身がコラムの中で言及しているというわけではありません。なのでこれに関する探究はここまでとして,河合自身がコラムの中で言及している事柄を対象とした考察に移ることにします。
繰り返しになりますが,『新科学対話』というのは,ガリレイの分身と思しきサルヴィヤチSalvyachiという人物が,弟子の質問に解答するという形式で進められていきます。その中に,もしAとBという2本の線がある場合,線の中には無限に多くのinfinita点が含まれているがゆえに,もしも線Aの方が線Bよりも長いのであれば,線Aに含まれている点の無限infinitumの量は,線Bに含まれている点の無限の量よりも大きいという見解に対して,サルヴィヤチが答えている部分が含まれています。まず河合はこの部分に着目しています。














