6÷2(2+1) の答えはいくつ

小学校の時、旅人算や鶴亀算を算数で学びます。　ところが数学 （ 連立方程式 ） で解くと簡単です。　わざわざ小学校で鶴亀算をやる必要があるのでしょうか ？。

　算数の落ちこぼれは、約分 （ 最大公約数 ） や通分 （ 最小公倍数 ） あたりから始まるそうです。　簡単に通過する、ようやく通過する、着いて行けない、に分かれて行く訳です。　孫の小 5 が今これをやっています。　上記の事が分かるような気がします。

　－－－－－－－－－－－－－－－－－－－－－－

　さて、話は変わりますが、次の計算式の答えはいくつでしょうか。

　6÷2(2+1)＝ ？

　孫の小学 5 年生は ９ と答えました。

　小 5 の回答、優先順 1 位の括弧をはずすと ６÷２✕３ と書き換えられます。

　÷と✕は左から順に計算します。

　間違ってますか ？。　間違っていませんよね。　答えは ９ になります。

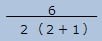　高 1 の孫の解法は ６÷２（２＋１）＝  と分数にし 分母の ２ と分子の ６ を約分し ３分の３＝１ と解きました。

　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　私の考えは （２＋１） を a として上式を書き換えると、６÷２a となります。

　数学では ２a は一つの数字として扱います。

　a＝３、２a＝６ ですから、６÷６＝１ となります。

　なんとしても答えを １ にしたいならば　６÷{２(２＋１)}＝１　とすべきではないのでしょうか ？。

　出題者の意図としては 「 ９ 」 が正解、「 １ 」 が不正解という引っ掛け問題だったわけなのですが、ごれが物議を呼び 「 １ 」 が正解という主張する人も多く、長い間 SNS や掲示板で議論を呼んでいた問題です。 

　皆さんは、１派ですか ９派ですか ？ ・・・ 数学研究者でも二派に分かれている 様で、 「 定義不足 （ 数式自体の書き方が間違っている ）  」 であるとして結論が出ていないらしいです （ 従って １ でも ９ でも正解と言えます ）。　数学遊びは面白いとおもいませんか？。

探偵はBARにいる・鉄道員（ぽっぽや）

　最近は乱読状態で一回に 3 冊買い込んで三日後にはもうブックオフに居ると言う生活をしております。　勿論、110 円コーナーですが。

　

　「 探偵は BAR にいる 」 はテレビ朝日の日曜劇場で観た事があるので、今更と思いながら買ってみたらなんと ・・・ 映画の原作は 「 探偵はバーにいる 」 ではなく 「 バーにかかってきた電話 」 という、シリーズ 2 作目の映画化だったのです。　「 探偵はBARにいる 」 は映画で 「 探偵はバーにいる 」 は小説だったと言う事です。　結果ダブらずに良かったと言うのか騙されたと言うのか微妙ではあります。　BAR とバーの違いでした （笑）。

　110 円コーナーの文庫本は単行本が出版されてから 7～10 年経っています。　今頃そんな本を読んいるの ？ と笑われそうですが、諸事情 （ ゲルピン ） により仕方がありません。

　お勧めの本があります。　第 117 回直木賞 （ 1997 年 ） を受賞した浅田次郎の 「 鉄道員（ぽっぽや） 」 です。　20 数年以上も前の作品ですから、今更とお思いでしょうが、110 円文庫本愛読者であり、読書と言う選択肢がなかった人生に 70 才にして突如として読書に目覚めてしまったのだから、読書愛好家の最後尾を周回遅れ （ 数周回遅れ？ ） で走っている様なものです。

　この本を手に取る前は、長編小説だと思っていました。　8 編の作品が収められている短編集 （ いずれも秀作 ） だったのです。　表題の 「 鉄道員 （ ぽっぽや ） 」 はたったの 38 ページです。　30 分もかかりません。　私は映画は見ていませんが主演を高倉健さんが演じているのは知っていたので、イメージを被せて読みました。　見事なキャスティングです。　二回読みました。　二回目も泣きました （笑）。　

　正しく " 奇跡の一巻 " （ 本書のあとがきより ） と言えます。　読書愛好家は既読 （ 140 万部を売り上げるベストセラー ） でしょうから、読書の取っ掛かりとして老後で暇を持て余している読書初心者にお勧めです。　「 ラブ・レター 」 「 角筈にて 」 いずれもティッシュペーパーを傍に置いて読んだ方がいいでしょう （笑）。

　

　最後に直木賞の選者の一人である、井上ひさしさんの一番辛口だと思われる書評を紹介しておきます。　「 粒選りの中でも、さらに高い質を誇っていた。 」 「 八つの短編が収められているが、うち四つは大傑作であり、のこる四つは大愚作である。　大傑作群に共通しているのは、「 死者が顕われて生者に語りかける 」 という趣向で、この趣向で書くときの作者の力量は空恐ろしいほどだ。　たとえば 「 角筈にて 」 を読まれよ。　この一編で、大愚作群の欠損は充分に埋められたと信じる。 」 と ・・・。

FB8XY eQSL

　今日、eQSL で FB8XY が CFM 出来ました。　1979 年の QSL ですから 42 年ぶりです。　既に紙 QSL をリアルタイムで受領済みです。　今頃どうしたんでしょうかね ？。　当時は紙ログだったでしょうから、デジタル化 ( ADIF化 ) は大変な作業だったのではないでしょうか。　頭が下がります。　皆さんの所にも来ているのでしょうか。　

　

　最後の行にチョット引っ掛かる言葉が ・・・ 。　
　QSL Confirmed 42 years after !! 73's QRO de Chris --- FB8XY
　これって私の QSL が 42年ぶりに先方に到着したって事 ？。　QRO って何 ？。　その返事が今日って事ですか ？。 　一体全体どうなっているのでしょう ？。

もうすぐ誕生日・耳鼻咽喉科に行った

■　もうすぐ誕生日です。　いよいよ ” 73 サヨナラ ” になります。　これからは、年毎にカウントダウンが始まるみたいで嬉しくありません。　お棺に入れて貰おうと思ってた QSL は先日、全部捨ててしまいました。　誤解がない様に申し上げておきますが、QSL は大切です。　決して QSL を否定して、おろそかにしている訳ではありません。　QSL の回収に於いては悲喜こもごもの想い出があります。

　何らかのアワードを狙っていて QSL を集めているのなら ・・・ ですが、今後そんな目標もないし、頂いた QSL は隅から隅まで拝見し、十分に楽しませて頂きました。　CQ 誌と同様に読み終わったら、処分してもいいのではないかと最近思う様になりました。

　わたしは、命の次に大事 ？にして来た QSL です。　開局当時の QSL なんてハガキです。　コールサインはゴム印、版画、隙間一杯にメッセージやリグの説明、家族の話しまで書いてあったりで涙が出ます。　こんな交信記念証を本当に捨ててもいいのでしょうか ？。　私はコンピュータで受領の記録は残しています。　データは USB に全て入っています。　はい、お棺に入れるとすれば USB です　（笑）。　あの世にパソコンとプリンターがあれば、あの世からでも QSL 発行できます　（笑）。

　付き合いの長い仲間、先輩、ローカルなど、シガラミのある QSL で捨てきれない QSL が相当あります。　しかし、これとて最後は同じ運命になるのです。

　そういえば、開局当時は QSL を靴箱に入れて 「 こんなにたまったぞ 」 とローカルに自慢してましたっけね。　QSL の運命はオーナーと共にあります。

■　耳が遠くなりました。　スタジオでは大音響で音楽を聞き、バンドではでかいアンプの爆音を聞き、自宅ステレオでも大音響。　ところが最近、娘家族と同居しました。　自宅ステレオの大音響禁止！。　しかたなく、ヘッドホンで大音響。　無線でもヘッドホンでノイズとの戦いと、一般人とは耳の使い方が違う人生を送って来ました。　やっぱり難聴になる確率は高いでしょう。

　1か月前から急に喉に違和感があり、声が出しに難くなりました、変な声が出ます、そこで耳鼻咽喉科に行きました。　すると鼻からスコープを突っ込んで声帯を画面でみせてくれます。　喉頭がんなどの心配はなく、加齢のためだと簡単に片づけられた。　加齢ならば仕様がない。　今、中学生以来、2 回目の声変わりを経験している。

J5T 14MHz CW

　約１年ぶりの DX Pedition カテゴリーの投稿です。　珍しく、本当に珍しく無線機の電源を入れました。　17 時頃です。　7MHz のアンテナが不調なので、14MHz を覗いて見る事にしました。　下の方からスイープアップして行きました。　何も聞こえません。　と、突然 14.034MHz で凄まじいパイルアップが起きています。　何だろう？。　ダイアルを少しづつ下へ ・・・ ご本尊 （ J5T ） いました。　14.032MHz です。　LP で、私の 2 エレでも S が 7 も振っています。

　

　少しの間ワッチしていました。　何年振りだろうこんなパイルアップは ・・・ なんてノスタルジーに浸っていたんです。　我に返り 「 呼んでみよう 」 あくまで ” 参加 ” の気持ちです。　JA がどんどんスキップし、一見パイルが小さくなった様な錯覚に陥りました。　J5T は相変わらず強力です。　「 行けるか !! 」 ・・・ 結果は ” 参加 ” のみで終わってしまいました。　諦めるのも早かったし、無線機の電源を落とすのも早かったです。　J5T は 22 日までやっているらしいので、明日も聞いて見ようと思っています。

　今日のリグは FT-1000MP でした。　デュアルワッチでスプリット側のダイアルをクルクル回しながらの ” 参加 ” でした。　スコープに慣れてしまっているので、不便さを感じながら呼びましたが、これが、また懐かしい、年齢と共に昭和にタイムスリップです。　もう、スコープなんか無くても 「 人力ワッチ上等 」 じゃないですか。

　QSO 出来た報告なら説得力もあるかもしれませんが、負け惜しみと取られても仕方がない ！ 。　でも意外に楽しめましたよ ・・・ 「 人力ワッチ 」 本当に 。　他人 ( パソコン ) 任せの無線より遥かに面白いと、改めて思いました。　

電気自動車 VS 水素自動車

　電気自動車を簡単に言ってしまうと、電池とモーターがあればいい。　と言う事になります。　つまり内燃機関などのノウハウが要りません。

　大手のメーカーは電気自動車がクリーンエネルギーである事は承知の上でも、電気自動車を許容する事が出来ません。　何十万人の従業員を抱えている大手では不用な部門が沢山出来るからです。　産業構造がガラリと変わります。　下請けにしても、得意分野とは違ったものにシフト出来なけれ生き延びれません。　

　今のハイブリッド車は規格をクリアできず認められません。　従ってトヨタは新しく 国の肝いり で水素で動くクリーンエンジン （ 内燃機関 ） を使用した水素自動車を開発しています。　

　しかしバッテリーの研究が進み、軽量かつ走行距離も 400㎞ をクリアし急速充電にも対応すると言う技術が確立されようとしています。　もうモーターとバッテリーとプラットホームが出来れば電気自動車は、ベンチャー企業であろうとすぐ作る事が出来ます。　トヨタは電気自動車にシフト出来ない内部事情があるので、軽自動車専門の自動車メーカーを囲い込み （ 傘下に置き ） 電気軽自動車を生産させ、成功を確かめて 「 やっぱり次代は電気でっせ 」 と水素自動車を諦める理由にするのか？。

　電気は何処でも充電でき、インフラの整備も容易く、災害時の停電にも車のバッテリーが役に立つなど水素ステーションを全国に新たに作るよりも優位です。　0.13mm の厚さのフィルム電池も日本で発明され、色んな所に自由に張り付ける事が出来るらしい。　軽量化にも繋がる。　どうも、次世代は電気自動車でしょう。　そのあと、水素自動車が来るの ？。

　世の中には生まれて消えたものがあります。　ベータ版 、VHS、miniDV、DVD、ブルーレイ、HDD。　レコード、カセットテープ、8トラック、MD、CD、メモリー ・・・ 等々。　赤文字はもう探すのが大変です。　近い将来はガソリンステーションは無くなって電気・水素ステーションになってしまうのでしょうか ？。

ウケ狙い？ 天然？ 悪ふざけ？

■　私の同級生がとんかつ屋で、「 ヒレ一口カツ定食 」 のメニューを見て 「 ひれーろかつ定食 ってなんですか ？ 」 と若い女子店員さんに尋ねたんです。　店員さんの肩が震えていたが、 「 あ、ひれひとくちかつ定食 ですね 」 と普通に対応してくれました。　店員さんが厨房に消えて奥の方から笑い声が聞こえて来ました。　この店員さん、お客さんの前で笑いをこらえるの大変だったと思います。　

　この彼は、中華料理屋で 「 みず餃子 （ 水餃子 ） 」 くださいと言い、スイーツ店では 「 ちち製品 （ 乳製品 ） 」 と読んだりするのです。　時々ウケ狙いなのか天然なのか分からなくなります。

■　19 歳の学生の頃、海水浴場で先輩と待ち合わせをしました。　海水浴場は広いので 「 どうやって探すのか ？ 」 と私が訪ねると、「 案内所の放送で呼んでくれ 」 と ・・・。　「 で、いいか、東京大学の一本松ポン太様、お友達が案内所でお待ちです 」 と呼んでもらえ。　こんな事を真面目な顔して言うんです。

　先輩には逆らえませんから、言われた通りにして案内所で待っていると、周りからの視線が痛く突き刺さります。　そこに 「 東京大学の一本松ポン太です 」 と本人登場です。　案内所は爆笑です。　この先輩はロックバンドのボーカルでこう言う ” おふざけ ” を何とも思ってない様子です。　こんな ” おふざけ・イタズラ ” を許容出来るかどうかは人それぞれでしょう。　年齢も関係してくると思われます。　勿論、悪ふざけと取られる事も承知の上の確信犯なんですが、こんな遊び、ん～～どうでしょう。

　因みに彼は日本大学でした。　当時は 「 ポン大 」 と呼ばれ、自慢できる大学ではありませんでした。　「 東京大学の一本松ポン太 」 は自虐ネタであり風刺ネタでもあるのです。

　しかし、この 「 ポン大 」 と言う呼び方は正しくありません。　何故なら、「 にっぽん大学 」 ではなく 「 にほん大学 」 なのであります。　要は 「 あんぽんたんの行く大学 」、即ち 「 ポン大 」 と言う事だったのでしょう。　あれから時代は半世紀も経っていますので、現在はこんな偏見は払しょくされているものと思います。　このネタにお怒りの諸先輩方、こんな ” おふざけ ” は東京大学生には出来ないと思いますよ。　全然余裕です。　日本大学万歳。

FT-CLEAN

　多分 50 年前くらいでしょう。　FT-CLEAN を覚えていらっしゃいますか？。　私は完全に忘れていました。　珍しいでしょ。

　

　YAESU のトランシーバー専用クリーナーです。　振って見たらチャポチャポと音がしますから、使用出来るかどうかは別として、何らかの液体が入っています。

　米国の製品でコリンズやドレーク専用のビニールのダスターカバーがありました。　使用しない時に被せて埃をかぶらない様にするものです。　今でも、埃だらけになった TS-520 , 9R59 , FT-101 等を所有している OM も多いかも知れません。　いざ電源を入れて見ると埃が焦げる様なヤバい匂いがしたりします。　どこかのガレージファクトリーでダストカバーを発売してくれないでしょうか？。　もう皆さん終活に掛かっていますから、今更の感はありますけれど ・・・。　JA にはそう言う発想はなかったのでしょうかね。