沸騰大変動時代（六十五）

彦根藩二代当主である井伊直孝公をお寺の門前で手招き雷雨から救っ
たと伝えられる招き猫と、井伊軍団のシンボルとも言える赤備え（戦
国時代の軍団編成の一種、あらゆる武具を朱りにした部隊編成のこと
）と兜（かぶと）を合体させて生まれたキラクタ「ひこにゃん」

【季語と短歌：６月２０日】

　　　　　　老鶯やダンプが吠える目覚かな　　

　　　　　　　　　　　　　　　　　　　　　 　　小見山　泉
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　龍・まいだ一ん　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　きぶし咲く

　　川に沿ふ志賀の山越のぼり坂いまはむかしの今道をゆく

　　  むらすずめ飛び立ちてのち突然の比叡おろしに雪しまきをり

　  　切り岸に並みてしだるる木五倍子の黄花わかち書きなる歌を思はせ

　　  手折りきて瓶に挿したる四行詩の枝のうれより青葉が出づる

　　  これの世に遺しし言葉ちりぬるを調ひをれば光たちきぬ

　　　　　　　　　　　　　　　　　　　

【ペロブスカイトPV向けの高機能材料を開発】
キヤノンは，ペロブスカイト太陽電池の耐久性および量産安定性を向
上させることが期待される高機能材料を開発。



【要約】
持続可能なエネルギーソリューションの探求において、ペロブスカイ
ト太陽電池は、その優れた効率性と費用対効果により有望な手段とし
て浮上。しかし、その広範な採用は、主にハロゲン化ペロブスカ
イト膜内のイオン移動と空孔形成に起因する性能低下の問題によっ
て妨げられる。イオン欠陥の影響を軽減するために、通常はキャリ
アのバリケードとして機能するパッシベーション層が使用。それでも、
直列抵抗の増加を避けるために極薄化が求められるため、製造プロ
セスが複雑になる。ペロブスカイト太陽電池の性能低下を軽減する、
ルイス塩基機能を持つp型有機半導体であるガリウムフタロシアニン
水酸化物（OHGaPc）をパッシベーション層として導入。この材料は
ルイス塩基であることによってハロゲン化物の空孔をパッシベーシ
ョンし、p型半導体として効率的な電荷輸送を促進することを実証。
 OHGaPc のこの二重の機能性は、ペロブスカイト太陽電池の安定性
と性能を向上させるだけでなく、極薄絶縁膜が不要になることで製
造プロセスを簡素化します。私たちの研究結果は、ルイス塩基と p 
型半導体の特性を活用して電荷抽出と全体的なセル効率を向上させ
ることの重要性を強調し、耐久性と効率に優れたペロブスカイト太
陽電池の開発に新たな方向性を示す。
【関連論文】
・Phthalocyanine-Based Polycrystalline Interlayer Simultaneously Realizin
　g Charge Collection and Ion Defect Passivation for Perovskite Solar Cells
・ https://pubs.rsc.org/en/Content/ArticleLanding/2024/TA/D4TA02491E

【最新ペロブスカイト太陽電池製造技術⑤】
❏ 特開2024-058455 電圧整合タンデム太陽電池モジュール 株式会
社 豊田中央研究所
【発明を実施するための形態】

【００５０】 単セルの電流密度ｊ（ｖ）は、定電流源、ダイオード、
直列及び並列抵抗の組み合わせからなる等価回路により数式（１）に

ように表される（J. Nelson, Physics of Solar Cells (Imperial College Press,
London, 2003)）。

【数１】
【００５１】 ここで、ｊｐｈは光電流密度、ｊ０とｎＩＤはそれぞ
れダイオードの逆飽和電流密度と理想因子、ｒｓとｒｓｈはそれぞれ
直列抵抗と並列抵抗である。ｑ，ｋＢ，Ｔはそれぞれ電荷素量、
Ｂｏｌｔｚｍａｎｎ定数、セル温度である。ｊｐｈは、セルの外部
量子効率ηＥＯＥ（ｈバーω）（ただし、ｈバーはプランク定数ｈを
２πで除した値）と太陽光の光子数スペクトルｎｓｕｎ（ｈバーω）
によって数式（２）で表される。
【数２】
【００５２】 ダイオードの逆飽和電流密度ｊ０のセル温度Ｔに対す
る依存性は、経験的には数式（３）のように表される（D. C. Nguyen,
F. Murata, K. Sato, M. Hamada, and Y. Ishikawa, Energy Sci.
Eng. 10, 1373 (2022)）。ここで、Ｅｇはバンドギャップである。
ｎ０，ｃ０はそれぞれフィッティングパラメーターである。
【数３】
【００５３】 ボトムモジュールにＣＩＧＳを用いる場合、集積化モ
ジュールの特性には、最表面の透明導電膜のシート抵抗ｒＴＣＯと、
透明導電膜／金属膜の接触抵抗ｒｃが影響する。ここでは、金属膜
としてＭｏ膜を適用した。一方、Ｍｏ膜のシート抵抗は透明導電膜
のシート抵抗ｒＴＣＯの１／１０以下であるから（S. Nishiwaki,
A. Burn, S. Buecheler, M. Muralt, S. Pilz, V. Romano, R. Witte, L. Krainer, 
G. J. Spuhler, and A. N. Tiwari, Prog. Photovolt.: Res. Appl. 23, 1908
 (2015)）、その影響は無視できるほど小さい。

【００５４】 単セルの電圧ｖｂのとき、位置ｘにおけるＭｏ膜とＴ
ＣＯ膜の間の電位差ｖ（ｘ）は、電位差ｖ（ｘ）に依存する電流密度
分布ｊ（ｖ（ｘ））と数式（４）で示す関係にある（M. Burgelman 
and A. Niemegeers, Solar Energy Mater. Solar Cells 51, 129 (1998)）。
ここで、ｗｂはボトムモジュールのセルの発電領域の幅である。

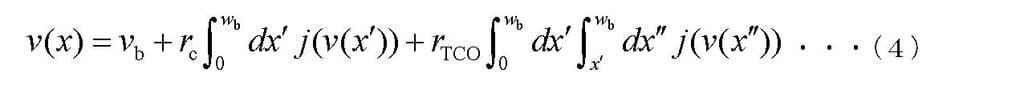
【数４】
【００５５】 数式（１）と数式（４）からなる連立方程式を解くこ
とにより電流密度分布ｊ（ｖ（ｘ））が求められ、更にこれから単
セルの単位長さあたりの電流ｊｂ（ｖｂ）（〔電流〕／〔長さ〕）
を数式（５）のように求めることができる。

【数５】
【００５６】ボトムモジュールにＰＶＫを用いる場合には、基板側
にも透明導電膜が用いられるので、その影響を考慮する。トップモ
ジュールについても類似の考え方により単セルの単位長さあたりの
電流ｊｔ（ｖｔ）を求めることができる。　
【００５７】同一のサイズの基板に、トップセル及びトップセルが
それぞれｎｔ，ｎｂ個集積化及び直列接続されたトップモジュール
及びボトムモジュールを形成し、トップモジュール及びボトムモジ
ュールを光入射方向に積層及び並列接続した電圧整合タンデム太陽
電池モジュールについて考察する。当該電圧整合タンデム太陽電池
モジュールの電流密度Ｊは、セル間の接続領域の幅ｄｔ，ｄｂは発
電に寄与しないことを考慮して、数式（６）のように表される。
【数６】

【００５８】変換効率ηは、電圧Ｖの関数としての出力Ｐ（Ｖ）＝
Ｊ（Ｖ）・Ｖの最大値と、入射光強度Ｐｉｎの比である。電圧Ｖを
ｎｔｖＶＭに置き換えても出力Ｐの値は変わらないので、改めて数
式（７）を定義する。

【数７】
【００５９】ここで、ｖＶＭは１つのトップセル当たりの電圧であ
り、ｎｂ／ｎｔは１つのトップセル当たりのボトムセル数である。こ
れを用いて数式（８）が得られる。
【数８】

図１３ 比較例の四端子モジュールの構成を示す図

【００６０】図１３は、比較例である四端子モジュールの構成を示す。
四端子モジュールの場合、トップモジュール２００及びボトムモジュ
ール２０２はそれぞれ独立に機能する。したがって、変換効率ηは、
トップセルの数ｎｔ及びボトムセルの数ｎｂには影響されず、数式（
９）で表される。
【数９】

【００６１】  図１４は、比較例である二端子モジュールの構成を示
す。二端子モジュールは、トップセルを構成する光電変換層１４と
ボトムセルを構成する光電変換層２４とを導電層３０を挟んで直接積
層して１つのモジュールとした構成を有する。二端子モジュールにつ
いては、トップセル及びボトムセルの２接合（２ｊ）単セルの電流密
度ｊ２ｊ（ｖ２ｊ）を数式（１０）の連立方程式を解くことにより求
め、これを用いて他と同様の手順により変換効率ηを求めることがで
きる。

図１４比較例の二端子モジュールの構成を示す図

【符号の説明】１０  基板、１２、第１導電層、１４  光電変換層、
１６  第２導電層、１８（１８ａ，１８ｂ，１８ｃ）  間隙、２０  
基板、２２、第３導電層、２４  光電変換層、２６  第４導電層、
２８（２８ａ，２８ｂ，２８ｃ）  間隙、３０  導電層、２００  
トップモジュール、２００ａ，２００ｂ  トップサブモジュール、
２０２  ボトムモジュール、２０２ａ，２０２ｂ  ボトムサブモジ
ュール。

【００６２】 トップセルとしてＰＶＫ（２５℃におけるバンドギャ
ップＥｇ＝１．６８ｅＶ）、ボトムセルとしてＣＩＧＳ（２５℃にお
けるバンドギャップＥｇ＝１．０８ｅＶ）を用いることを想定し、そ
れぞれの単セルの電流密度ｊ（ｖ）を以下のようにして定めた。
【００６３】  ２５℃における外部量子効率ηＥＯＥ（ｈバーω）に
はＰＶＫ／ＣＩＧＳ積層の二端子モジュールについての実測値を用い
た（M. Jost, E. Kohnen, A. Al-Ashouri, T. Bertram, S. Tomsic,
 A. Magomedov, E. Kasparavicius, T. Kodalle, B. Lipovsek, V. 
Getautis, R. Schlatmann, C. A. Kaufmann, S. Albrecht, and M.
 Topic, ACS Energy Lett. 7, 1298 (2022)）。また、ＰＶＫのバン
ドギャップＥｇの温度係数ｄＥｇ／ｄＴ＝０．３ｍｅＶ／Ｋ
（O. Dupre, B. Niesen, S. De Wolf, and C. Ballif, Phys. Chem.
 Lett. 9, 446 (2018)，E. Aydin, T. G. Allen, M. De Bastiani,
 L. Xu, J. Avila, M. Salvador, E. Van Kerschaver, and S. De 
Wolf, Nat. Energy 5, 851 (2020)）、ＣＩＧＳのバンドギャップ
Ｅｇの温度係数ｄＥｇ／ｄＴ＝－１ｍｅＶ／Ｋ（M. Troviano and 
K. Taretto, Solar Energy Mater. Solar Cells 95, 3081 (2011)）
を考慮して外部量子効率ηＥＯＥ（ｈバーω）の温度Ｔへの依存性
を求めた。そのうえで、数式（１）により表される電流密度ｊ（ｖ）
が実測値に近い値となるように、ダイオードの理想因子ｎＩＤ，直
列抵抗ｒｓ，並列抵抗ｒｓｈ及びフィッティングパラメーターｎ０，
ｃ０を決めた結果を表１に示す。【００６４】【表１】

                                                この項つづく



【大規模気象変動と食糧安全保障①】
「リスク・インパクト・マネイジメント」としての「食料安全保障」
の諸施策の考察は、ブログ考察で掲載しているから参考されたし。

【風瀟々と蒼い時代】

the beatles evolution of music (1962-2023)





● 今日の言葉：心の中も衣替え