やっと流れがつかめた今日この頃(理解の速度が遅いなあ!)
「今回も海の編集室」さんのお世話になります。 http://atl-publishing.com/blog/serial/post-621/
●陸の目標が一つしかない場合
四点方位法、船首倍角法、両側方位法(ランニングフィックス)などがあり、それぞれ基本的な考え方はほぼ同じ。
四点方位法と船首倍角法について簡単に説明し、その後で実用性が高いランニングフィックスの手順を説明しよう。
いずれも二等辺三角形の性質を使ったもので、船は同じ進路、同じ速度を維持するのが前提になる。
ネットで調べて見てもちっとも読んでいないね。ただ上っ面だけしか見ていない。何回か見ているうちにやっと理解が出来た。
四点方位法、

船の進行方向(針路)から45度の位置にある物標を探し、時間と船の速度を記録しておく。
そのまま進んで、物標が真横に来たときの時間を記録する。 その間にかかった「時間×速度」で船が移動した距離がわかり、それはそのまま物標との距離にもなるので、船の位置が決まる。
・船首倍角法
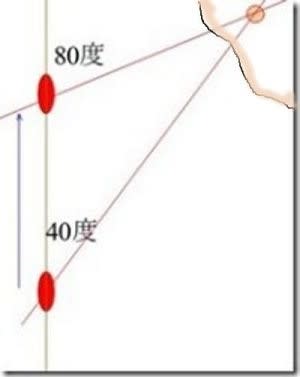
船の針路から物標までの角度を測り、時間と速度を記録しておく。 そのまま進んで、物標がさきほどの角度の2倍になる位置に来たところで時間を記録する。
その間の「時間×速度」が物標までの距離になるので、船の位置が決まる。
手順は四点方位法と同じだが、角度が45度に限定されないので利用可能な状況が増す。 これも二等辺三角形の性質を利用してますね。
●ランニングフィックス
 これがちょっと良く分からないね。
これがちょっと良く分からないね。
1.A点で、物標の方位と時間を記録する。
2.船の進行方向と方位の線を海図に線で引く。
方位線はコンパスローズを使って正確に引くが、
進行方向の線については物標からの距離はだいたいでよい。
3.そのままの方向と速度でしばらく進んでから、もう一度物標の方位を測定し、その方位の線を海図に記入する。
4.進んだ時間×速度で出た距離の分だけ、最初の点Aから測って進行方向の線に印(B)をつけ、Bが2番目の方位線と重なる位置まで線分ABを進行方向の線に対して平行移動させる。 その点が船の位置になる。
●六分儀を使って距離を知る

薄紫の線は人間の高さね
船から見えるところに島や山がある場合、その高さを六分儀で測ることで船の位置を知ることもできる。 左図で、山頂直下までの距離を x m、山の高さを h m、仰角をΘとすると
Tan Θ = h / x これを整理すると、
距離 m =h / tanΘ 天測計算表には三角関数表も掲載されているので手計算でも可能だが、関数電卓を使うと手っとり早い。
山頂から方位の線を引き、計算した距離の分で印をつければ、それが船の位置になる。数字はメートルなので、海図上でディバイダで距離を移す場合は、海里に直しておく。 1海里=1852m
でも太平洋とか大西洋の海のど真ん中で自分の所在地を確認するのはどうするんだろうね?。
















