拙著「音律と音階の科学」などは,二つの楽音の協和を,不協和曲線に基づいて説明している.
二つの単音(単一周波数の音)の音高が一致すれば違和感がないが,少し離れると違和感が増し,十分離れれば違和感が消える...という前提から出発し,楽音の周波数スペクトルのデータを使ってごちゃごちゃ計算すると,完全4度,完全5度,長3度,長6度などが協和することが導かれる.
もっと仮定を単純化すると,「音高が一致するふたつの単音以外は,聴いて違和感がある」ということになる.逆に言えば,どこかで同じ音が鳴っていれば,高さが違う音を同時に鳴らしても親しみを感じる.
例えば,楽音のドと楽音のソが協和するのは,楽音ドにミが含まれているからだ.
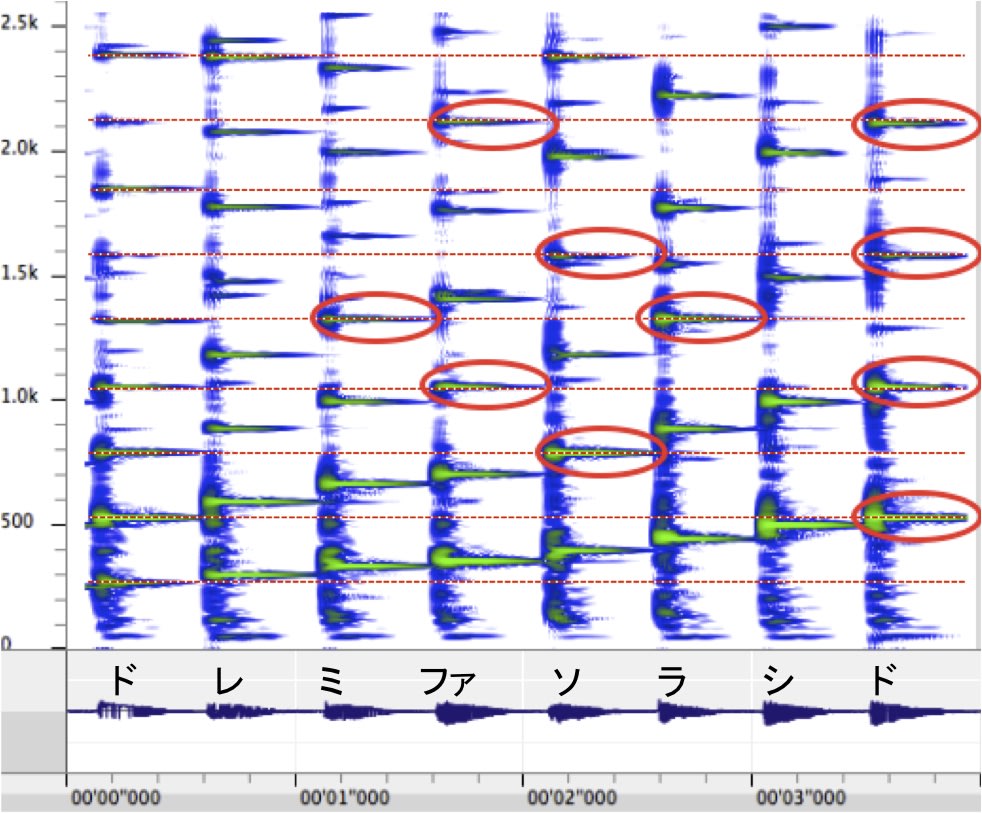
この図はピアノでドレミファソラシドを弾いたときのソノグラム = 周波数スペクトルの時間変化を表示するもの.横軸が時間,縦軸が周波数.左端を上下方向に見ると,ドというキーを押し下げたとき,266Hzがいちばん低い周波数成分として出ている.これがドの音である.しかし,その他に,2倍波すなわち2x266Hz,3倍波すなわち3x266Hz,4倍波すなわち4x266Hz...が上方向にずらずらと並んでいる.
その隣の縦列はレの周波数スペクトルで,やや大きい間隔で縦に並ぶ.その右はミだが,間隔はもっと広がる.
ドの各周波数成分の位置を横方向の点線で示してある.
これで見ると,ドの下から5番目とミの下から4番目は 縦方向に同じ位置にある.ここを赤丸で囲む.
隣の,ファの3番目はドの4番目と同じ位置にある.ここも赤丸で囲む.
おっと,ファの6番目もドの8番目と同じ位置にある.ここも赤丸で囲む.
エトセトラ.
要するに,レ,ミ,ファ,ソ...のうち赤丸の数が多い音ほど,ドと同時に弾いたときの響きが良い,すなわち協和度が高いことになる.
もっと詳しく言うと,赤丸の位置が低いほど協和する.
この図では,ドと協和する音を順位づけると,オクターブ上のドがいちばん良く,ソ,ファと続き,ミとラが同列となる.
このようにうまいこと赤丸が描けるのは,じつはミ,ファ,ソ,ラの最低音の,ドの最低音にたいする周波数比が単純だからである.平均律ではじつはずれているのだが,ご覧のようにスペクトルにも幅があるので誤摩化される.
しかし12音平均律で音階を作るからうまく赤丸が描けるのであって,例えば16音平均律などでは赤丸はひとつも描けない.
もともとの周波数音の他に,その2倍波,3倍波,4倍波,...が生じるのは,ピアノだけでなく,多くの管楽器・弦楽器の音に共通している.2倍波3倍波4倍波...がないと音楽の音としてはつまらない.ただし,打楽器の音にはまた別な規則性があり,ガムランのような音楽には,この説明は通用しない.
長文失礼いたしました.
二つの単音(単一周波数の音)の音高が一致すれば違和感がないが,少し離れると違和感が増し,十分離れれば違和感が消える...という前提から出発し,楽音の周波数スペクトルのデータを使ってごちゃごちゃ計算すると,完全4度,完全5度,長3度,長6度などが協和することが導かれる.
もっと仮定を単純化すると,「音高が一致するふたつの単音以外は,聴いて違和感がある」ということになる.逆に言えば,どこかで同じ音が鳴っていれば,高さが違う音を同時に鳴らしても親しみを感じる.
例えば,楽音のドと楽音のソが協和するのは,楽音ドにミが含まれているからだ.

この図はピアノでドレミファソラシドを弾いたときのソノグラム = 周波数スペクトルの時間変化を表示するもの.横軸が時間,縦軸が周波数.左端を上下方向に見ると,ドというキーを押し下げたとき,266Hzがいちばん低い周波数成分として出ている.これがドの音である.しかし,その他に,2倍波すなわち2x266Hz,3倍波すなわち3x266Hz,4倍波すなわち4x266Hz...が上方向にずらずらと並んでいる.
その隣の縦列はレの周波数スペクトルで,やや大きい間隔で縦に並ぶ.その右はミだが,間隔はもっと広がる.
ドの各周波数成分の位置を横方向の点線で示してある.
これで見ると,ドの下から5番目とミの下から4番目は 縦方向に同じ位置にある.ここを赤丸で囲む.
隣の,ファの3番目はドの4番目と同じ位置にある.ここも赤丸で囲む.
おっと,ファの6番目もドの8番目と同じ位置にある.ここも赤丸で囲む.
エトセトラ.
要するに,レ,ミ,ファ,ソ...のうち赤丸の数が多い音ほど,ドと同時に弾いたときの響きが良い,すなわち協和度が高いことになる.
もっと詳しく言うと,赤丸の位置が低いほど協和する.
この図では,ドと協和する音を順位づけると,オクターブ上のドがいちばん良く,ソ,ファと続き,ミとラが同列となる.
このようにうまいこと赤丸が描けるのは,じつはミ,ファ,ソ,ラの最低音の,ドの最低音にたいする周波数比が単純だからである.平均律ではじつはずれているのだが,ご覧のようにスペクトルにも幅があるので誤摩化される.
しかし12音平均律で音階を作るからうまく赤丸が描けるのであって,例えば16音平均律などでは赤丸はひとつも描けない.
もともとの周波数音の他に,その2倍波,3倍波,4倍波,...が生じるのは,ピアノだけでなく,多くの管楽器・弦楽器の音に共通している.2倍波3倍波4倍波...がないと音楽の音としてはつまらない.ただし,打楽器の音にはまた別な規則性があり,ガムランのような音楽には,この説明は通用しない.
長文失礼いたしました.















