たぶん高校理科で登場するリサージュあるいはリサジューは,2つの周期振動を平面で直交させたときの点の軌跡が描く図形.2つの振動数比を,たとえばド音とソ音の振動数比にあわせると,わりとシンプルな図形になるので,「だからドとソは協和する」と言ったりする.個人的にはこうした絵は,描くのも視るのも好きだが,音との関係に深い意味があるように言うのはいかがなものか, と思っている.
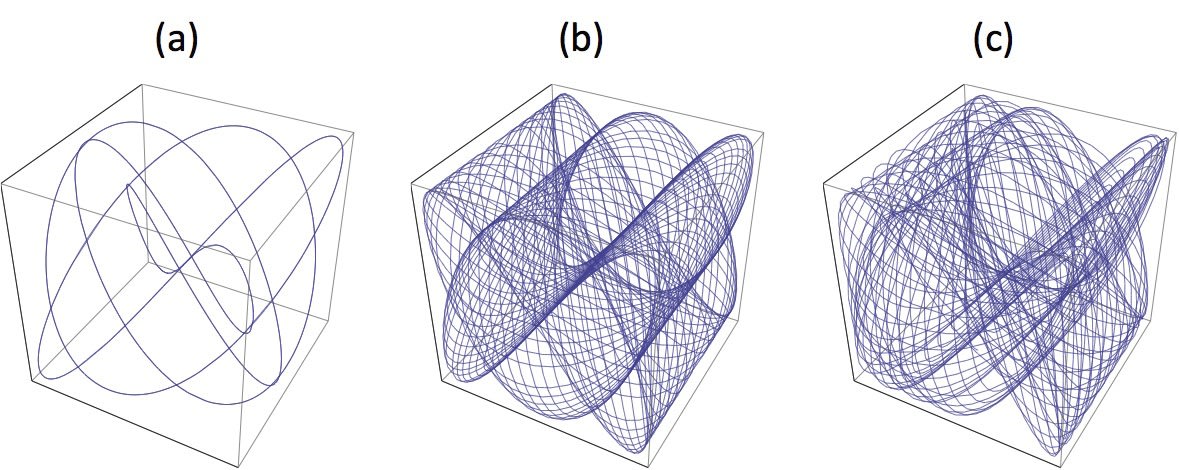
さて3つの周波数を対象にするとリサージュも3次元になる.これは(a)純正律,(b)ピタゴラス音律,(c)平均律の,それぞれのド・ミ・ソの周波数比で描いたもの.
ここでは,点の座標を(x, y, z) = (sin t, sin Et, sin Gt) とし,E の値は純正律では5/4=1.25,(b) のピタゴラス音律では 81/64=1.2656..., (c) の平均律では 12の4/12乗 = 1.2599... とした.またG は純正律とピタゴラス音律では3/2=1.25,平均律では 12の7/12乗 = 1.4983... とした.t の範囲は0 < t < 120π とした.t の上限を∞に近づけたかったが,そうすると平均律の図(c) は真っ黒になってしまう.
純正律は当然シンプル.ピタゴラス音律ではド・ソ平面への投影だけがシンプル.平均律はごちゃごちゃである.
ハーモノグラフ (http://blog.goo.ne.jp/ablerail1007/e/8ca70d5f00943e7ee575f1aa988e0a98) は2次元リサージュを複雑にしたものだ.

さて3つの周波数を対象にするとリサージュも3次元になる.これは(a)純正律,(b)ピタゴラス音律,(c)平均律の,それぞれのド・ミ・ソの周波数比で描いたもの.
ここでは,点の座標を(x, y, z) = (sin t, sin Et, sin Gt) とし,E の値は純正律では5/4=1.25,(b) のピタゴラス音律では 81/64=1.2656..., (c) の平均律では 12の4/12乗 = 1.2599... とした.またG は純正律とピタゴラス音律では3/2=1.25,平均律では 12の7/12乗 = 1.4983... とした.t の範囲は0 < t < 120π とした.t の上限を∞に近づけたかったが,そうすると平均律の図(c) は真っ黒になってしまう.
純正律は当然シンプル.ピタゴラス音律ではド・ソ平面への投影だけがシンプル.平均律はごちゃごちゃである.
ハーモノグラフ (http://blog.goo.ne.jp/ablerail1007/e/8ca70d5f00943e7ee575f1aa988e0a98) は2次元リサージュを複雑にしたものだ.















