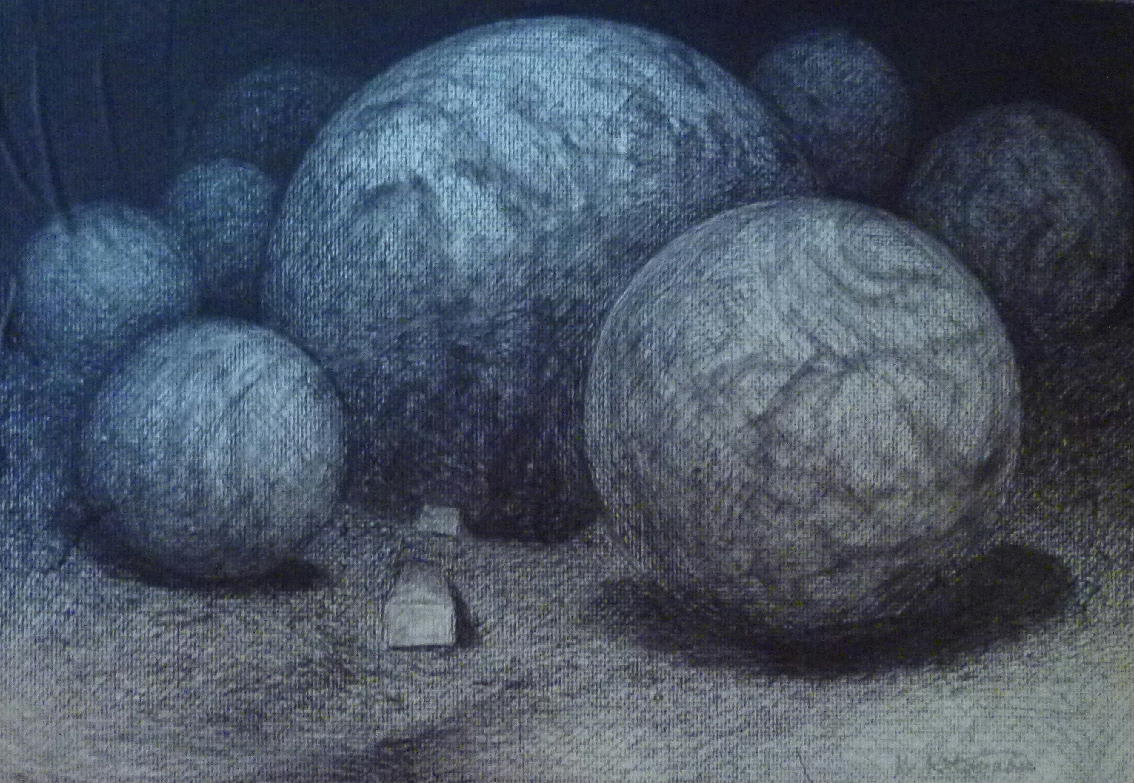私たちが認識する極小の世界。原子。
これはたとえば、こんなイメージですね。
そして極大の世界、宇宙。
上の2枚の図は、悠久の世界(i-Mart)に掲載されています。
私はこの2枚の図はスケールの違う世界ですが、おなじ性質を持った世界だと考えます。
次の私の図は、スケールの世界を表したものですが、一定のスケールごとに、おなじ性質の世界が現れてくる、螺旋の . . . 本文を読む
私のかつての上司だったMさんに上本町ギャラリーに来ていただいて、ゆっくり絵の鑑賞をしてもらいました。
私にとっては、そのあとの対談に気持ちが行ってしまって、Mさんが接待の茶を飲み干すのを待って、「行きましょうか」と立ち上がったら、「おいおい、まだ絵を観てないよ」というのが対談の始まりでした。
Mさんは居合の有段者(確か8段)で、上司と部下の関係で職責をになった3年間に、体と気に付いて、武術の視 . . . 本文を読む
今回は、空間にある光について考えてみたいと思います。
現在進行形の私の絵です。キャンバスにシャーペンで描きますが、線一本で無から石ころが生まれてきます。すると空間が動きます。その表情の変化が楽しいのです。
照明を消すと真っ暗になります。私には何も見えません。絵はなくなったのでしょうか。
そんなことはありませんね。私にはわかっています。照明を付ければまた絵を描き始めることが出来ることを。
. . . 本文を読む
E=mc2
有名なアインシュタインの数式です。E=エネルギー M=質量 C=光速ということで教えられましたが、もちろん私にはどんな理論が背景にあるのかわかりません。
しかしとても心引かれる数式です。芸術的に見ても美しいと思います。そこで私はこの数式に芸術的な解釈をしてみようと思ったのでした。
エネルギーとは何なのかということです。
物質(M)とは、その内部にある空間のエネルギーに引き寄せら . . . 本文を読む
次元という言葉が難しいと聞きました。確かに、普段はあまり使わない、なにか難しい学術用語のように聞こえます。そんな言葉を聞いた途端、身をただすか逃げるしかない。
ですがどうか安心してください。私の使う次元という言葉は、私たちが普通に感じる事を言っているにすぎません。私自身学者とは縁遠い芸術家ですので、理科、数学は高校どまりです。
その芸術家が一番わからんと言われれば、立つ瀬はありませんが・・・
. . . 本文を読む
なぜ絵を描くのか、そう問われれば、それは人として常に最前線を生きなければならないから。そう答えるしかありません。
人は生まれたときから閉ざされた己の空間の中に心を成長させます。そして今あるこの場所とこの瞬間がその心の最前線であることを5次元思考は常に教えてくれるのです。
先日は心の大きな要素である認識の源流を遡って考えてみましたが、今回はその逆をたどってみたいと思います。
この図の一番下に . . . 本文を読む
今日は私たちの認識の仕組みについて考えてみましょう。認識という言葉を難しく考えないで下さい。普通にものがあることを知り、それが何であるかを知ることです。
机の上に何かがあります。何でしょう?
「机の上に白いコップがある。」私たちはこの写真を見てそう答えます。誰もがそう認識しますね。
話がややこしくなりますので、この際、机と白いという認識は置いといて、「コップがある」という認識だけを考えて . . . 本文を読む
寒い日が続きます。早朝の浜は、強い寒風にさらされて激しい波が打ち寄せています。明け方の闇の海面から闇より黒いものが山のように盛り上がります。その頭が崩れて白いものがあっという間に私の足元に広がってきます。
自然の意志を直に感じるようで、なにか対話している気分になる。
私たちはこのように外の風景を、認識します。
そして同時に、私は自分の内側にこみあげてくる緊張感を味わっています。この内側の認識 . . . 本文を読む
世界と言うと、あなたはどんなイメージを持つでしょうか。
真っ先に地球上にある国々。あるいは宇宙。自分を取り巻く世界、あるいは社会。それを逆に見れば、自分という存在の外側の世界ということになりますね。
そして自分=「私」という存在は、この世界の中で生きているのです。私たちは意識的であれ無意識であれ、この世界という認識と、「私」という認識を明確に区分しています。
わざと、当然のことを遠回しに言っ . . . 本文を読む
前回はスケールを極小に向かって無限に続く物と空間のつながりを観てきましたが。今回は逆に極大に向かって考えてみましょう。
空間に浮かぶものたちは互いに引きあって1なる存在をつくり続けます。それは極大に向かっても同じことがいえるのです。
私たちには宇宙の銀河と見えるものは、それと相当のスケールで見れば一つの細胞に見えるでしょうし、その銀河が無数に広がっている銀河は、ひとつにまとまって見えるスケール . . . 本文を読む