
原発は核分裂に伴うエネルギー放出の利用である.
図は原子核の結合エネルギーの質量数との関係で,鉄 Fe あたりで最大となる.鉄より軽い核種は融合してエネルギーを放出することができ,鉄より重い核種は分裂してエネルギーを放出することができる.例えばウラニウム U の核分裂で利用できるエネルギーは,理想的な場合で (実際はもっと小さい) このグラフで U の縦軸と Fe の縦軸の,それぞれの値の差である.
核分裂は (核融合も!) 不可逆過程であるから,エントロピーを増大させる.これを計算して,火力発電の場合と比較してみたいとは思うのだが,どうしていいかわからない.
50 年以上前の大学の熱力学ではエントロビー S=Q/T と定義していたが,核分裂の場合熱 Q って何? 温度 T って何? という疑問から先へは進めない.
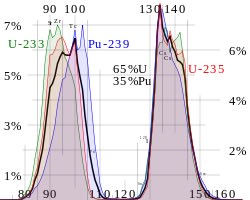
核分裂で,もとの原子核はこなごなになってしまう.これは原発で熱中性子によってウラン235 (グラフでは赤) .プルトニウム239 (青)) およびトリウム燃料サイクルにおいてウラン233 (緑) が核分裂を起こした場合の核分裂生成物の収率を,横軸を質量数として示したものである.山がふたつできるのが特徴.
統計力学が定義するエントロピーは W を状態の数として,S=klnW (k はボルツマン定数) であって,W を核分裂生成物の状態数と考えれば感覚と合う.しかし同じ不可逆過程でも核融合の場合は,例えば D+T→4He+n で,このような発想で状態数を定義してもうまくいきそうにない.
熱力学はマクロな,統計力学はミクロなアプローチと考えれば,この問題を考えるには熱力学が適しているように思える.アマゾンであたったところでは,
- 田崎晴明 『熱力学―現代的な視点から』(2000) 培風館(新物理学シリーズ) ISBN 978-4-563-02432-1.
- 清水明 『熱力学の基礎』 (2007)東大出版会 ISBN 978-4-13-062609-5.
あたりから勉強しなおす必要がありそう.
しかし気が進まない.物理屋は素核屋と物性屋に分類でき,前者はたいていエントロピーが苦手である.自分は二者の境界を泳いできたのだが...
ふたつのグラフはhttps://ja.wikipedia.org/wiki/核分裂反応によります.















