池越えのパー3のホールに来ました。ティーグランドには205ヤードとその距離は
書かれていますが、ほぼ真直ぐなフラッグまで、ティーグランドからの距離を測る
場合、どのようにすればよいでしょうか?
江戸時代の伊能忠敬が日本沿岸海與地全図を17年かかって完成させたときの測量
方法は、要所に立てた梵天を目標として、もっぱら歩数(歩幅)、鉄鎖、間縄による
導線法という方法だったそうですが、このパー3のホールのように池越えの場合は
どうすればよいか?
ティーグランドの両端、例えば20m離れたところから、フラッグを観た時の角度
を測定し、それの縮尺を図面に書いてフラッグまでの距離を求める。三角測量ですね。
ティーグランドの中心から、左右に10mずつ離れてフラッグを覗いた時の角度が、
それぞれ87度であった時、下図の縮尺図(1/2000)から、ティーグランドからグリ
ーンのピンまで、図の上で実測(9.5㎝)し縮尺を戻すと約190mとなります。
パー3のホール(a-c=0.5㎝ c-p=9.5㎝ 図ではこのようになっていませんが)

この場合、懐かしい三角関数 tanθを用いると簡単ですね。 上の例ですと、
ティーグランドとフラッグで構成される二等辺三角形の中線に着目して、△acpは
直角三角形ですから
tanθ=ac/pc ここで、θは∠apcで、これは、元の2等辺三角形の頂角∠apbの
1/2ですから、 ∠apb=180°―87°×2=6° なので θ=3°となります。
tanθ=tan3°=0.0524 で、ac=10m ですから、
tanθ=ac /pc に代入すると、
0.0524=10/pc これから pc=10/0.0524 =190.8 となります。
ティーグランドからフラッグまでの距離は約190mとなります。

これはショートホールを例としましたが、ロングホールでは、縮尺図を作成して
実測するのはもはや、フラッグまでの距離が長くなって作図がしにくくなるうえ、
ティーグランドからフラッグを覗いた時の角度がかなり微妙で、角度の差が大きな
距離の誤差となってしまいます。
天体などのもっともっと遠くの星などの距離はどのように測定しているのでしょ
うか?
先日(4/14)のニュースで『およそ131億光年かなたの遠方宇宙に潜む、塵(ちり)
に覆われた非常にコンパクトな天体が、ハッブル宇宙望遠鏡、すばる望遠鏡などの
宇宙望遠鏡や地上望遠鏡による観測画像から発見されました。』(国立天文台、研
究成果より)とありました。131億光年というのは、光の速度で131億年かかる距離
にある天体のことを言っているのです。
地球からの天体までの距離は、月:1.3光秒(光の速度で1.3秒=38万㎞)、太陽:
8光分(1.5億㎞)、火星:13光分(2.3億㎞)、金星:8光分(1.5億㎞)、シリウス:
8.7光年(80兆㎞)、ペテルギウス:500光年(5000兆㎞)

国立天文台のページに、大まかな測定方法として、天体の距離の測定方法があり
ました。そのままコピペします。
- 銀河系の中の近くの星までの距離は、三角測量の原理を使って測定すること
ができます。 - 星の色からは、その星の本当の明るさがわかります。星の本当の明るさと見か
けの明るさを比較することで、その星までの距離が推定できます。 - 近くの銀河などの場合には、星の本当の明るさと色の関係に加えて、その銀河
の中にある脈動変光星という星を使うことによって距離を推定します。 - 遠くの銀河などの場合には、銀河の中にあらわれる超新星を基準の明るさとし
て使うことで距離を推定することができます。 - 非常に遠くの銀河までの距離は、その銀河が遠ざかる速度を使って推定します。
まず、1の三角測量については、冒頭のゴルフ場での測量と同じです。しかし、
天体ですから、ゴルフ場の時のa、b間の距離をかなり広く取らないと、遠い目的の
天体までの距離に大きな誤差が生じる可能性があります。 そこで、このa、b点を、
地球の夏と冬にあてるのです。たとえば、夏至と冬至とすれば、太陽を中心として、
それぞれ半径が地球の公転半径となります。つまり、a、b間の距離は、公転半径=
約1.5億㎞×2となります。
ゴルフ場で、測定した時のティーグランドでの10mが、1.5億㎞に相当すること
になります。 で、夏至と冬至に、目的とする天体を見た時の角度を測れば、目的
天体までの距離が求められるのです。
地球から太陽や金星が丁度1.5億㎞ですから、夏至、冬至における角度は45°と
なりますね。
θは年周視差とよばれていて、太陽や金星では、θ=45°で、tanθ=1 ですね。
2にあるように、銀河系のもっと遠くの天体までの距離を測定する方法は、星の
色と明るさから推定します。 例えば太陽と同じ色の天体は、元々同じ明るさだと
仮定して、今測定する天体の明るさを太陽と比較して、明るさは距離の2乗に反比例
することから距離を推定するのです。
銀河系の外のもっと遠いところの天体の測定は、3や4、5の専門的な方法で測
定するというのです。
季節外れですが、冬の大三角形を形作る星座を見てみます。
冬の大三角形
 (ネット画像より)
(ネット画像より)
この中のオリオン星座は、あの見慣れた形ですが、立体的には、それぞれの星ま
での距離が相当離れているのですね。 いつも見ているのは、これらの星をあたかも
スクリーンに投影した時の形として見ているということなんですね。
オリオン座を立体的にみると
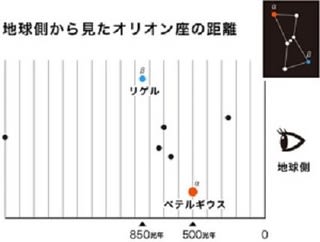 (宇宙兄弟HPより)
(宇宙兄弟HPより)
このところずっと、コロナやウクライナなど心が萎える現実にあって、たまには
これらと全く無関係な話題にひと時触れてみるのはどうかと思いました。
この測定で、三角測量の基点から対象物を覗く2つのポイント(ゴルフ場でのaと
b点)を、太陽を中心とした地球の公道の2点を選んだ知恵者が昔どこかにおられた
のですね。
8K空撮夜景 SKY WALK サンプルムービーvol.2 ロングバージョン【4K Ultra HDブルーレイ】【ブルーレイ】

















