黄金比 （bon）

　　　　関東地方は、今日は晴れましたが、このところ雨交じりのどんよりとした涼しい
　　　7月とは思えない日が続いていますので、気がつきませんでしたが、夏の高校野球の
　　　地方予選がすでに始まっていて、ココ埼玉でも、大宮、上尾、朝霞など多くの球場で
　　　混戦が繰り広げられています。新聞報道記録によれば、5回コールドで32対0という試合
　　　があったり、１インニングで19点というのもありました。
　　　　わが母校は、大阪で1回戦を突破しました。グラウンドに響く、若い元気な声を想い
　　　出しています。

　今更なぜ、黄金比？　という感じですが、ある時、蓼科農園に行った時の夕食後の団欒で、
この「黄金比」の話が出て、ひととき議論が盛り上がったことがありました。　メンバ―の
中に、黄金比にご信奉の人がいて、彼のメルアドにも、その黄金数1.618 を入れているほど
で、以前には“まさか黄金比の数字”とは気がつきませんでしたが、今頃になって、それが
黄金比であることが分かったのです。

　　　　　　パルテノン神殿
　　　　　　（㈱アーティスHPより）

　そんなことで、今更ではありますが、以下にちょっと整理してみました。起源はギリシャ
時代と言いますから、かなりの歴史を持っている自然の安定した美意識の一つなんですね。

　例によって、ウイキペディアから、黄金比は

　　　　　　　

 『線分を a, b の長さで 2 つに分割するときに、a : b = b :(a + b) が成り立つように
分割したときの比 a :b のことであり、最も美しい比とされる。』とあります。

 　a：b＝b：（a+b) から、b²＝a(a+b) が成り立ち　→　a²＋ab－b²=0 となり、a=1　と
おけば、b²- b – 1=0 で二次方程式ですね。

  二次方程式　x²-x－1=0　の正の解は　x = 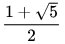          ですから、すなわち 

　　　　黄金数　               となります。

 

　一般に数学において、貴金属比は、　　　　　　　　　　　　　　

 　　　　　　　　　　で表されます。　したがって、

n が自然数の時、第 n 貴金属数は、

 　　　　　　　　　　　で表されます。

 

　ここで、第1貴金属数（ｎ＝１のとき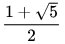）　　　　を黄金数

 

　　　　　第2貴金属数（ｎ＝２のとき）　　　　　を白銀数

　

　　　　　白銀比には、もう一つ１：√2　があり、この白銀数は√2となります。

 

そして、第3貴金属数（ｎ＝３のとき）　　　　を青銅数と呼ばれているのです。　

　　　

　また、第ｎ貴金属数は、連分数で左のように表され、したがって黄金数は右のように
表されます。

　　　　　　　　　 

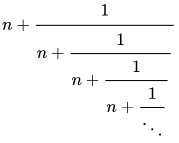
 　どこか美しい式ですね。

　余談になりますが、1：√３　を白金比と呼ばれているようです。　これは、貴金属比
ではなく、正三角形の1辺の１/2と高さの比で定数です。　白金数＝√３＝１．７３２・・　
ですね。この比もバランスが美しく、五重塔や木造建築などの比に現れているとありました。

 

　久し振りに数式などが出て来て、頭が重くなったかもしれませんね。

　黄金比に戻って、これを発見したのは　『古代ギリシャの数学者「エウドクソス」（紀
元前408年頃～紀元前355年頃）と言われており、その後パルテノン神殿の建設にて総監督
を務めたとされる彫刻家「ペイディアス」が初めてパルテノン神殿建設時に黄金比を用い
たと言われています。』とあり、　ずっと後になって、『ドイツの数学者マルティン・
オームが1835年に刊行した著書の中で「黄金比」という用語が初めて登場し、人類が最も
美しいと感じる比率として「黄金比」が広く知れ渡るようになった。』そうです。

　　　黄金比の作図　　　　　　　　　　　　黄金らせん　

　　　　　　　　　　　　　　　　　　　（いずれの図もウイキペディアより）

　なぜ「黄金比」と命名されたかについては、ネットで見つけられませんでしたが、おそ
らく、この黄金比は、正5角形や黄金らせんなどで、花びらや巻貝など自然界にたくさん
見られ、その安定した美しさ、さらには、数式の単純な姿の美しさから「黄金」と名付け
られたのではないかと想像しています。　白銀比や青銅比は後付で黄金に対した命名なん
でしょうね。

　欧米では、この黄金比が最も美しいとされているようですが、日本では、白銀比のうち、
√２＝1.4142・・が、より好まれているとの見方もあるようです。用紙のサイズ、A、B版
は、この白銀比なんですね。
　つまり、たて・よこ比が１:1.4の用紙で、半分にしても必ずこの比が保たれているので
すね。

　ずいぶん長くなってしまいました。お疲れさまでした。