量子の世界 （bon）

　昨今、量子コンピュータの話題をよく耳にすることがあります。先ごろ（2019.11.10）の
朝刊（読売新聞 暮らしとサイエンスページ）にも、このことがほぼ一面に解説されていま
した。　グーグルが発表した論文には、スパコンで1万年かかる数学的問題を、グーグルの
量子コンピュータは3分20秒で解いた・・などが出ていました。

　以前から、量子コンピュータや量子暗号などの記事に触れて、その都度「量子力学」の
難しい説明を読みながら、理解できず落胆したままでした。　今回も、まだまだ、理解でき
ていないことには変わりないのですが、これまでの既存物理（物質の性質、法則）とは違っ
た世界であることが何となくわかりかけてきたような感じがして、解明していないまま、
現状を記事にしてみました。　
　ですので、記事をお読みいただく方々には、明快に表現できていないだけでなく、やはり
わからないことだらけのままですので、大変お見苦しく、ご迷惑であることをあらかじめ
お詫びする次第です。

 

　量子というのは、ご存じの原子核とか、電子とかの原子を構成する要素を言います。例え
ば、電子が一つだと水素（H）、2つだとヘリウム（He）、３つではリチュウム（Li）4つは、
ベリリウム（Be）‥という具合に、たくさんの元素があります。で、これらの元素が組み合
わさって、あるいは反応して物質ができていますね。　ところが、量子（陽子、電子、中性
子，光子）のような、原子より小さいミクロの世界では、量子は、物質ではなく、状態だと
いうのです。　

　昔から、ずっと頭にある原子は、図に書くと、真ん中に原子核があって、その周りにいく
つかの電子の粒がまわっている・・。そんな絵ですが、電子は粒ではなく、状態だといい
ますから下図のように、雲のように描かれている方がより実態に近いようなんです。そして、
観測したとたんに、電子は、その雲状のどこかにある・・だから、通常、その場所にある
確率で表されるのです。

　　　　　　　原子モデル（ヘリウム）
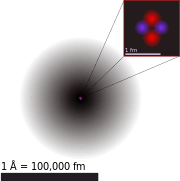 　　　　　　　（ウイキペディアより）

 

　で、量子には不思議な性質があるのですね。

　・量子は、粒子であるとともに波動でもある
　・重ね合わせ の性質がある
　・量子もつれ という性質がある

　ここで、超簡単にそれぞれについて説明しますと、

　粒子と波動の両方の性質：　二重スリットの実験（文末の動画をご覧ください）　光で
よく理解しているように、それは粒子でもあり波動でもあるというのです。

　重ね合わせの性質：　これまでの（古典）コンピュータでは、0か1のどちらかの状態しか
とりえなかったですが、量子は、0の状態と1の状態を、同時にとることができるのです。
例えば、コインが回転しているときには「表」と「裏」が未決定の状態で、表・裏のどちら
の状態もありえて（回転中という状態）、それが止まって倒れた時、すなわち観察した時に
はじめて表か裏かがわかる。この回転中で、観察するまでどちらかかわからない状態を
「重ね合わせ」と呼んでいるのです。

　量子もつれ（量子エンタングルメント）：先ほどの1粒子の重ね合わせが2つペアになった
状態の特別な場合で、たとえば、ペアになった粒子Aと粒子Bのそれぞれのスピンの向きが
「Aが上向き・Bが下向き」と「Aが下向き・Bが上向き」との重ね合わせ状態を形成している
場合に、一方の粒子を観測してその状態が分かれば、もう一方の粒子の状態は観測するまで
もなく、決まってしまうということなんです。かりに、Aが下向きだと観測されれば、その
瞬間Bは上向き状態に決まります。これは状態の瞬間収縮により瞬時に起こります。そして、
エンタングルメントの関係にある2つの粒子は、どんなに離れていても、この性質を示すの
です。
　　　　　　　　量子もつれ の可視化
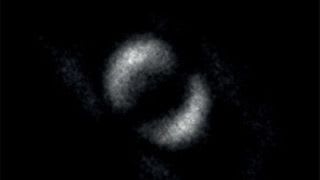　　　　　　　　（WIREDより）

　量子ビット　　重ね合わせによる量子コンピュータの情報単位のことを、「量子ビット」
(quantum bit＝キュービット：qubit)といいます。古典的（これまでの）コンピュータでは、
ビットは１，０で表されます。　量子コンピュータのビットは |0＞、|1＞ のようにケット
と呼ばれる特殊な括弧の記号を使って表現されています。これは古典ビットの0、1とは違い、
いわゆる量子状態を表しており、1つの量子ビットは、|0＞と|1＞が同じ確率で重なり合った
状態をとります。ただし、重なり合った状態が保たれるのは、誰も見ていない状態（観測さ
れていない時）に限られ、その状態を観測すると50％の確率で|0＞に、50％の確率で|1＞に
なるのです。量子力学では、これを測定による状態の収縮と言うそうですが、実は、これが
量子計算にとって重要な要素だというのです。

　京都産業大学のページには、『　古典ビットは、例えば、3つ並べた＜000＞や＜010＞と
いった個々の情報を個別にしか扱えせん。しかし、量子ビットでは、|000＞から|111＞まで、
8つの全ての状態を同時に扱えるのです。40個量子ビットを並べれば、扱える状態は1兆にも
なります。この1兆個の状態に対してある処理を行うと1兆個の重ね合わさった全ての状態に
対して並列的にその処理が行われます。

　もちろん、1兆個の状態で同時に処理が行えたとしても、一度測定すれば、その中のどれか
1つの状態が確率的に選択されてしまいます。それでは意味がないので、最終的に、欲しい答
の状態だけを取り出すために、欲しい答が測定により選択される確率を高めることが必要に
なります。このように、量子計算では測定が決定的な意味を持ち、測定という処理に至るまで
にいかにして重ね合わせ状態を効率よく処理するかを考えるのが量子アルゴリズムの研究です。』

　並列に処理する・・というのも難しいですが、量子は、いろんな状態が重なり合って存在
しているので、その性質を利用して、計算を一気に、全部同時に行うのが量子コンピュータの
発想なのだそうです

　実用性があると言われる量子アルゴリズムは、現在、2種類だけで、一つは、ショアのアル
ゴリズムといって、大きな桁数の素因数分解に威力を発揮するアルゴリズムです。そしてもう
一つが、多数の組み合わせから最適な解を求めるための グローバーのアルゴリズムです。

　素因数分解は、普通 に計算する時は2で割って3で割って・・と進めますが、量子コンピュー
タでは 2で割った状態も3で割った状態も重なり合って一度に処理できる ためにスピードが
速いのですね。で、この目的を達成するための仕掛け？が、ショアのアルゴリズムなんです。
だから、専用的な処理に特化していますが、例えば、長い桁数の素因数を用いた暗号の解読に
使われると、簡単に解かれてしまう事態になり大変となります。これに対抗する、量子暗号を
開発する・・などに発展するでしょう。

　もう一つのアルゴリズムは、「量子アニーリング方式」（量子焼きなまし方式）と呼ばれ
るもので、考えられる組み合わせの中から最適なものを選び取る「組合せ最適化問題」の
計算に特化した技術です。
　たとえば、巡回セールスマンが、多数の場所を訪問する際に、コスト（移動時間や交通費）
を最小化する経路を探索する問題です。仮に、10軒の顧客を巡回するとしたとき、古典コン
ピュータだと、順番に一つ一つのルートを計算して、その結果最適なものを選ぶ‥となります
が、これだと、１０！（階乗）つまり、10×9×8×・・で、362万通りの計算となり、平均で
もその半分、もし、12軒だと、その数は4億通りとなり、とてつもなく大きな数になってしま
います。
　しかし、量子コンピュータでは、重ね合わせともつれの特性を利用して、360万の可能性す
べてを同時に検討し、その上で、量子力学的な波動特性を利用して、最善の回答が見つかる
まで異なる可能性の取捨選択を行う・・というのですが、このところがよく理解できません。

　要するに、このような処理ができるように、超微細加工技術で量子を一列に並べて、絶対
0℃の中で、電気信号により変化するチップを作り、このアルゴリズムが遂行できるように
実装する・・？ということなんでしょうか？

 

　今度こそはと取り組んでみましたが、核心に来ると、ユニタリー行列やアダマール変換など
の数式が出てきて、やはり数学的な力量がないと十分な理解が得られないことがわかりました。　
　なので、概念的、直感的な見方しかできず、ミクロの量子世界の振る舞いを具体的に理解
することを諦めざるを得ない・・ことが分かりました。

　原子の内側と外側で、まったく異なる法則が働いているということなんですね。　そして、
この原子の内側の世界が、量子の世界で、これまでの因果律ではどうも理解しづらいのです。

　負け惜しみを言えば、“でも、以前よりは、少しは踏み込めた” ような気がしています。

 

　ネット勉強で、次のような解説がありましたので、youtubeから文末に掲載しました。

• 二重スリットの実験
• シュレディンガーの猫

　なお、量子力学の基礎については、下記をご参照ください。　
　　http://www.ryoushi-rikigaku.com/eigen_state.html