孫とのお正月 （bon）

　これまで何度も巡ってきたこの時期の過ごし方は、
当然ですが、年々成長と共に大きく変化していることに気づきます。

　今年のお正月では、孫は高1と中2（の女の子）で、その遊びもいわゆる双六やかるた（昔はいろはかるた、
昨年は歴史人物かるた）などは全く要求されず、ゲーム的なものでは、トランプ（7並べとかババ抜き、マジックなど）が
根強い人気の他、　新しく百人一首が主流となりました。
百人一首といえば、私の場合は高校になって、学校の授業にもあったりして初めて興味が出て　家族の仲間入りを
したように記憶していますが、今頃の子は既に中2で6~7割は、“上の句”　つまり出だしを詠んだだけで、
字札を取ってしまいます。　
以前は単純なゲームだけでしたが、今年などはどれも白熱するというか、どうかすると既に負けているのでした。　
体力などは、さらに明らかに差があることを認識させられます。　
毎年、近場ですが初詣と称して出かけますが、長時間立ったままだったり、長く歩いたりすれば、こちらは
アゴが上がってしまいますが連中は平気なんですね。

　パソコン画面の文字の読み取りや、マウス操作などの速さは全くついて行けません。
持参してきた　“お絵かきアプリ（ソフト）”　も自分でインストールして、何時間も向かって絵を描いているのです。

　休み中の宿題も持参してきていて、姉妹が並んで一定時間取り組んでいる時が、小生にとってはその時ばかりは
静かで平穏な時なんですね。　　時折、“この問題が分かんない！”　と、お呼びがかかります。　
大体が数学や理科なので、こちらも安閑としていおれるのです。

　数学で、グラフや確率の問題のいくつかは、問題集の例題などをヒントに何とか答えられましたが、一つだけ、
回答が出来なかった　“図形問題”　がありました。　
これは、私の宿題として、後日ようやく答が出ましたが、図形問題なので電話で伝えにくく、奮闘してパソコン
（ワード）で解答を作成してメール添付しました。

皆さん、久しぶりに挑戦してみてはいかがでしょうか？

 

問題です。

　三角形ABCの辺の長さが、図のようにAB=4、BC=2、CA=3 であり。
頂点Aの外角を2等分する線分とBCの延長線と交わる点をQとしたとき、

線分CQの長さ　ｘ　の値を求めよ。
                                       

  ちょっと、考えてみられてはいかがでしょうか・・・ 
　　　　　　　　　　　　　　　　　　　　　　　（私なりの回答を文末に載せていますのでご参考までに。） 

                                      

　　　　　　　　　　　　　　　　

 

 

考え方と答えです。

　線分ACに並行な点Qを通る線分を引き、値3の点をPとする。
また、線分BAの延長線上で点Aから値3の点をRとする。
AC∥PQ、CQ∥APで四角形ACQPは平行四辺形である。

　一方、∠RAQと∠AQPは等しく、かつ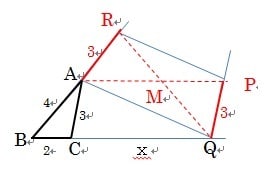　　　　　　　　　　　　　　　　　　
線分AR＝QP＝3で、四角形AQPRは等脚台形である。
この等脚台形の各頂点を結ぶ線の交点をMとする。

 

ここまでが、補助線を使った準備段階です。ここからが回答へ一直線・・。

 今、三角形RBQに着目して、底辺BQと辺AMの関係を求めれば、辺BQ＝２＋xだから、ｘを求めることができる。
では、線分AMはどのように表すことができるか？

AM∥BQだから、三角形RBQの辺RQは、RM：MQ＝３：４となりますね。
等脚台形の対角線等しく、RQ＝AP　かつ、AM＝MQとなる。
APは、平行四辺形ACQPだからAP＝CQ＝ｘ　である。

RM：MQ＝３：４　で、RQ＝ｘ　だから、RM=３/７・ｘ、MQ＝４/７・ｘ　となる。

 ここで、三角形RBQに戻って、

① AM：BQ＝３：７　であるから、AM、BQに数値を代入する。

　　　　　AM＝MQ＝４/７ｘ　、　BQ＝２＋ｘ　であるから　①に代入して

 ４/７ｘ：（２＋ｘ）＝３：７

　　　３・（２＋ｘ）＝４/７ｘ・７

　　　　　　６＋３ｘ＝４ｘ　　⇒　　ｘ＝６（答え）　　　　　

 

　簡単でしたか？