小学校の算数の問題です。
まず、最初に注意しておきますが、小学校では方程式も分数の掛け算も習っていませんので、それを使わずに問題を解いてください。
Q1:
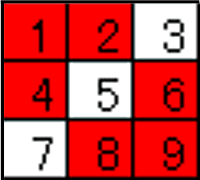
1から9までの数字が書いてるカードが1枚ずつあります。
これを、A君、B君、C君の3人に、3枚ずつ配ったところ、3人とも、カードを足した合計の大きさが同じになりました。(2年生問題)
A君は1、B君は2と4を持っていました。
C君のカード3枚をこたえてください。
A:1・□・□
B:2・4・□
C:□・□・□
Q2:
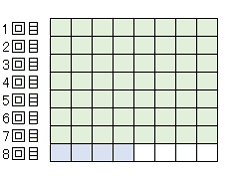
あなたは、10段ある階段の登る前の状態にいます。
「3歩上がったら2歩下がる」というルールで階段を上るとき、一番上の段に行くまで、全部で何歩歩くでしょう?(2年生問題)
Q3:
1から6の数字を1つずつ使って、次の空欄を埋めてください。(小学2年生問題)
□+□+□+□=□□
Q4:
小型のトラックに同じ大きさの荷物60個を、1度に8個ずつ運びました。
何回運べば運び終わる?(3年生問題)
Q5:
2mの棒があります。
これを5等分したうちの2つ分は何mか、分数で答えてください。(4年生問題)
Q6.
次の式を、「できるだけ簡単な式に変形して」答えを出してください。(5年生問題)
97×123-92÷4×97
Q7.
次の□に、+、-、×、÷のどれかを入れて式を完成させてください。(5年生問題)
18□3□2□4=13
正解は↓に!!
正解は↓に!!
正解は↓に!!
正解は↓に!!
正解は↓に!!
Q1:
1から9までの数字が書いてるカードが1枚ずつあります。
これを、A君、B君、C君の3人に、3枚ずつ配ったところ、3人とも、カードを足した合計の大きさが同じになりました。(2年生問題)
A君は1、B君は2と4を持っていました。
C君のカード3枚をこたえてください。
A:1・□・□
B:2・4・□
C:□・□・□
A1.答え
C君のカードは「3・5・7」
|
解説 まず、1から9までを全て足してみます。 1+2+3+4+5+6+7+8+9=45 合計45ということは、それを3人で分けると45÷3=15 つまり、一人当たりの合計が15になれば良いということに気づけばあとは簡単です。
A:1・□・□ B:2・4・□ C:□・□・□
まず2個数字が分かっているB君は、2+4+□=15なので、9が入ります。
A君は9が使えないので、残っている数字3,5,6,7,8で14になる数字を選びます。 1+□+□=15ですから、6と8が入ります。
C君は、余った、3と5と7(足すと15)となり、正解が導けます。 |
Q2:
あなたは、10段ある階段の登る前の状態にいます。
「3歩上がったら2歩下がる」というルールで階段を上るとき、一番上の段に行くまで、全部で何歩歩くでしょう?(2年生問題)
A2.答え
38歩
|
解説 もちろんこれも、1つずつ数えていっても解くことはできますが、考え方として、まず押えるべきは、「3段上がって2段降りる=5歩」ということ。 つまり、5歩で1段上がるということです。 これを7回繰り返すと、7段目に立ちます。ここまで5×7で35歩です。
残り3歩ですから、35+3で38歩になります。 (8回繰り返してしまったら、10段目まで行った後に2歩下がるところまでカウントしてしまいますのでちゅういがひつようです。) 小学校低学年の応用問題は、大人が使えるような公式などはほとんど習っていないため、工夫で問題を解くことが多いです。 |
Q3:
1から6の数字を1つずつ使って、次の空欄を埋めてください。(小学2年生問題)
□+□+□+□=□□
A3.答え
2+3+4+6=15
解説
はっきりとした計算方法は無いのですが、ポイントは、1から6の合計(21)を考えると答えの十の位は「1」しか入らないことに気づきます。
あとは、一の位に入るものを1つずつ確認していくしかありません。
答えを「12」にすると残り3+4+5+6=18≠12✕
答えを「13」にすると残り2+4+5+6=17≠13✕
答えを「14」にすると残り2+3+5+6=16≠14✕
答えを「15」にすると残り2+3+4+6=15=15◯
Q4:
小型のトラックに同じ大きさの荷物60個を、1度に8個ずつ運びました。
何回運べば運び終わる?(3年生問題)
A4.答え
8回
|
解説 60÷8=7あまり4 大人の人はあまり引っかからない問題だと思いますが、小学生の頃は、「7あまり4回」とそのまま書いてしまった人も多いはず。 最後の1回は4個運べばいいことに気づけば簡単です。
|
Q5:
2mの棒があります。
これを5等分したうちの2つ分は何mか、分数で答えてください。(4年生問題)
A5.答え
5分の4m
|
解説 これは、引っかかりやすい問題です。 「5等分のうちの2つ」と聞くと、5分の2と答えてしまう小学生が多いのです。 「2mのうちの」というところまで理解できていれば、2倍する必要があることが分かります。 5分の2m(2/5m)だと40cmということになります。 2mの棒の5分の2は80cmですから5分の4mになります。単位がmだということに注意が必要です。
あなたは引っかからず解けたでしょうか。 |
Q6.
次の式を、「できるだけ簡単な式に変形して」答えを出してください。(5年生問題)
97×123-92÷4×97
A6.答え
97×123-92÷4×97
=(123-92÷4)×97※
=(123-23)×97
=100×97
=9700
|
一見すると、100というシンプルな数字は出てこなさそうですが、()を使って1つずつ処理していくと、暗算でも普通に解けるレベルの式に変えることができます。 ※普通に考えると(97×123)-(92÷4×97)なのですが、問題第に「できるだけ簡単な式に」とあるので()でくくった中に×97が2つあるので1回に省略するという考え方です。 |
Q7.
次の□に、+、-、×、÷のどれかを入れて式を完成させてください。(5年生問題)
18□3□2□4=13
A7答え

|
解説 計算感覚が一番の武器になります。 基本的には感覚で記号を入れていくしかありません。 しいて考え方をあげると ①まず18の後ろに×を入れると大きすぎる(54)ので除外します。 ②÷を入れても6で、その後13にはなりませんし、他の2つの空欄も、÷を入れると少数になってしまうので入る確率は少ないので÷を除外します。 ※①.②によって、最初に×が入らず、全てに÷が入らない、という前提から考えるのです。①、②ののように確率の低いものを除外して、できるだけ少ない回数のチャレンジで正解を導き出すといいと思います。 |
いかがでしたでしょうか。
子供のころも、こんなに頭を使っていたわけです。

したっけ。













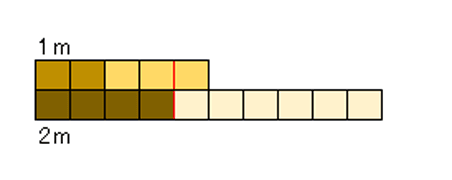



















低学年では寝ないでしょう。
算数は公式を使わないと難しいですね^^
したっけ。
したのであればその時 絶対寝てましたね(笑)
高学年の問題の方が解きやすかったです^^
柔軟な頭で発想しないと解けませんね。
ありがとうございます。
入選作は来年載せますよ^^
したっけ。
こういう問題を方程式を使わないで説いていたんですよ。
6番はできるだけ簡単な式にというところが悩むところです^^
したっけ。
頭痛くなっちゃいました~^^
Q1、Q6、Q7はわかりました^^*
ご入選おめでとうございます。
ほんとうに素晴らしいですね。
6番迷いました。
掛け算、割り算が先は覚えてましたが、余計ヤヤコシイ式に替えて×。
私子どの頃の方が回転良かったんだ(笑)
さて!草刈に参ります。大人は仕事で勝負(*^^*)