竹内薫著『素数はなぜ人を惹きつけるか』(朝日選書503(素数)、2015年2月28日朝日新聞出版発行)を読んだ。
「数」の中でもっとも基本的な元になる数である「素数」。この素数の不思議な性質、出現のバラツキ具合を解りやすく解説し、素数の不思議に対する数学者の挑戦の歴史を語る。
後半は、数式が登場して難しくなる。ただ、この本の数式は計算するためのものでなく、鑑賞して楽しむものだそうだ。
また、13年周期あるいは17年周期で大量発生するセミ(蝉)、原子核のエネルギー準位や、超ひも理論、さらには音楽と素数が関連すると紹介される。
「双子素数」(「5」「7」のように差が 2 である2つの素数)
「三つ子素数」(「5」「7」「11」のように間隔が2や4である3つの素数)
「いとこ素数」(「3」と「7」のように差が4である2つの素数)、
「セクシー素数」(「5」と「11」のように差が6である2つの素数)
たとえば、アメリカのある地域では、13年周期か17年周期で大量発生するセミが存在する。このセミはある一定周期で発生するため「周期ゼミ」と呼ばれているが、素数の年に大量発生するため、別名「素数ゼミ」とも呼ばれている。なぜ13年や17年といった素数年ごとに大量発生するかといえば、それがセミにとって有効な生き残り戦略であるためだ。
小さくて栄養価の高いセミは、捕食者に狙われやすいが、いくら食べられても生き残る個体がある一定数だけ存在すれば、絶滅を免れることができる。そのために彼らが取った手段が、素数周期ごとの大量発生。素数以外の周期で発生するセミも存在していたが、偶数年に現れるセミは、生存戦略上、とても不利だった。たとえば12と8の最小公倍数は24。12年と8年の周期で大量発生するセミがいたとすると、24年毎に発生時期が重なって交雑が起こり、発生する周期が乱れてしまうため、生き残り戦略を取ることができなくなってしまう。素数ならば、他の数との約数を持たないため、最小公倍数が大きくなり、同時発生する間隔が大きくなる。13年と17年であると、時期が重なるのは、221年後であるから頻繁に発生時期が重なることは考えにくく、生存戦略上有効であるようだ。
目次
第1章 素数を知れば、数学へのイメージが変わる
第2章 素数を知れば、日常のカラクリが見える
第3章 素数の歴史を知れば、人類の挑戦が見えてくる
第4章 リーマン予想が解ければ、歴史が動く
第5章 素数を知れば、宇宙の成り立ちがわかる
第6章 素数の見方を変えれば、その美しさが見える
コラム
1. 素数の英語は「prime number」
2. ゴールドバッハ予想とは何か
3. 冗句としての素数――ネットに溢れる異常な愛情
4. 和算と素数の関係はいかに?
5. ガウスは人類最高の数学者かもしれない
6. リーマンって超有名人?
7. チューリングが残したもの
竹内薫(たけうち・かおる)
1960年東京生まれ。サイエンス作家
東京大学理学部物理学科卒。マギル大学大学院博士課程修了。
『99.9%は仮説』『数学×思考=ざっくりと』など
私の評価としては、★★★★(四つ星:お勧め)(最大は五つ星)
後半難しい数式が登場するが、厳密には理解できなくても、形だけで雰囲気、おおよその形態、複雑さが分かり、楽しむとはいかなくても、文章だけより解りやすかった。あるいは解った気分になれた。
本文も、ユーモアある文章でわかりやすく、楽しく書かれている。また、コラムでより幅広く、深く素数を理解できるよう配慮されている。
以下、メモ
ゴールドバッハの予想(まだ証明されていない)
4以上の偶数は少なくとも一通りの2つの素数の和であらわすことができる。
なお、3つの素数を足すと7以上の奇数を表すことができる。
ミレニアム懸賞問題(解けば1000万ドルもらえる)
リーマン予想を含む未解決問題は6つ。ポアンカレ予想は解かれた。
オイラーの等式(世界一美しい数式)
eiπ+1=0
Polymath
数学の専門家や愛好家が集い、集合知を使って数学の問題に挑戦するインターネットの互助組織
リーマンの素数公式
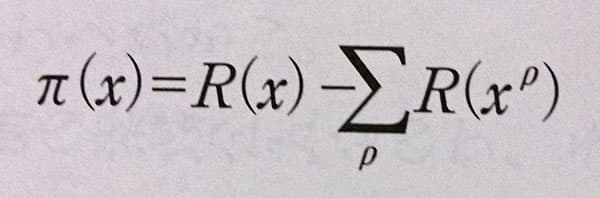
π(x) は素数の個数関数で、x 以下の素数の個数、ただし、和はゼータ関数の複素零点 ρ 全体をわたる。
R(x) はリーマン関数















