先日に続き、『フィボナッチのうさぎ』から。※参照※12月2日のブログ
「ピックの定理」というのが載っていました。
点の数を数えて面積が求められるそうです。
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
多角形の内点の数をIとし、境界点の数をBとすると、多角形の面積は、式
I+B/2-1
によって与えられるのだそうです。
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
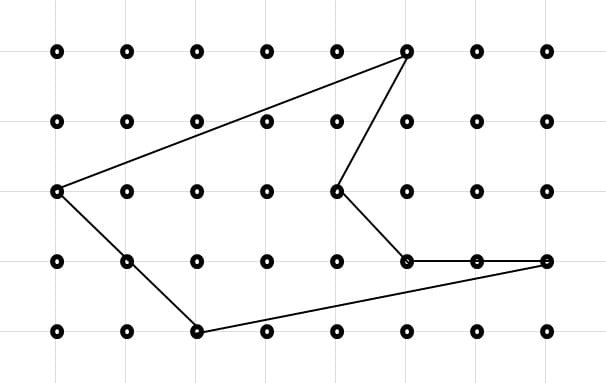
Iは8、Bは8
I+B/2-1=8+4-1=11
大きな四角形から多角形以外を外していくと、
28-(5+2+5/2+6+3/2)=28-17=11
同じです。
単純な格子多角形、つまりその境界が自分自身と交わらない格子多角形ならば、ピックの公式は必ず適用できる(全ての角が格子点上にない場合はピックの公式は適用できない)そうです。
「ピックの定理」というのが載っていました。
点の数を数えて面積が求められるそうです。
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
多角形の内点の数をIとし、境界点の数をBとすると、多角形の面積は、式
I+B/2-1
によって与えられるのだそうです。
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

Iは8、Bは8
I+B/2-1=8+4-1=11
大きな四角形から多角形以外を外していくと、
28-(5+2+5/2+6+3/2)=28-17=11
同じです。
単純な格子多角形、つまりその境界が自分自身と交わらない格子多角形ならば、ピックの公式は必ず適用できる(全ての角が格子点上にない場合はピックの公式は適用できない)そうです。















