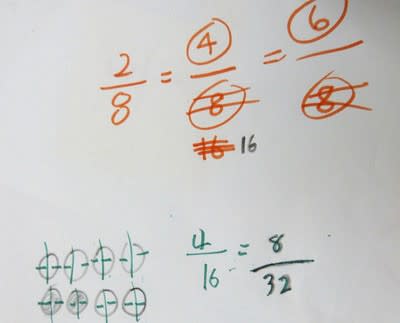忍者好きの子たちとした活動の様子(過去記事です)
をいくつかアップすることにしました。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
『ブロックで忍者屋敷』

年中のAくんと年長のBくんといっしょに忍者屋敷を作りました。
(AくんとBくんのお母さんたちにも手伝っていただきました。)

武家屋敷のからくりの一つです。
途中までしか階段がないので落ちてしまう危険な廊下。
下にはとがった竹が……!

手前の黄色い部分は『刀かくし』です。

『刀かくし』の床をめくると、刀が隠してあります。

『どんでん返し』です。

Bくんはブロック制作や工作がとても得意な子です。
天井から降りてくる梯子を作っています。


一休さんやきっちょむさんのとんち話が大好きなAくん。
忍者の逃げ方や隠れ方の知恵にとても興味を持っていました。
↑は、『水とんの術』水中に隠れて、そのまま逃げます。

他に『木とんの術』や
『火とんの術』なども再現して遊びました。

手裏剣を折っているBくん。

何を作ろうかと『忍術・手品のひみつ』を熱心に見ていたBくんは、
忍者の剣に目をとめました。
ブロック人形に剣を持たせるのでは物足りなかった様子です。
割り箸をつないで、自分用の剣を作っていました。

バッチリ決まっていますね。


『おしいれ』という板を押すと地下道への
入口が開くからくりです。

字を書くのがブームのBくん。

算数タイムに推理ゲームをしました。

トランプや手を使った計算遊びも面白かったです。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
『忍者屋敷のどんでん返し』
NHKの大河ドラマの『真田丸』。
子どもたちにも人気があるみたいですね。
教室で大阪城に出かけて以来、歴史に興味を持つようになった子がたくさんいます。
新年中~新年長の子らのレッスンで、(新小3のお姉ちゃんも参加)
忍者屋敷のどんでん返しを作ることになりました。
「大きくて自分たちが通れるのがいい」と言うので、ちょうど
サイズの大きいダンボールをいただいたところなので、子どもたちと
どんでん返し作りにチャレンジすることにしました。

自分たちの身体のサイズに合わせて、とびらの四角を切り抜いて、
とびらを半分に分けた位置に伸びるポールを貼ります。

回転とびらの横の長さの半分の位置にしるしをつけているところです。
ものさしを使わず、ポリひもを使って半分の位置を測ったのが印象的だったようです。

「( ポリきもを)半分に折ればいいのか!」と感動の声。
-------------------------
前回の記事で紹介した『マイコー雑記』というブログの
という記事で、こんな話題が紹介されていました。
---------------------------------
ある調査では、科学、テクノロジー、エンジニアリング、数学 の分野で高い成果を収めた人々は、
平均的なアメリカ人よりも、実践的なクラフトや趣味についての広範囲な体験を持っているとのこと。
例えば、木工、メカニックス、電子機器を用いた活動など。
一生を通してこうした活動に従事する人は、
特許を認可されるような発明品を生み出す傾向にある、とのこと。
「子どもたちのモノづくりの体験を、これからも応援していきたい」と強く思いました。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー

前回の続きは、近いうちに書きますね。
どんどん溜まってくる写真を、とりあえずアップしていきます。
年長さんの★くんが作っていた『忍者屋敷』です。
板をスライドすると……床が抜けて……


この通りまっさかさま。

何の変哲もない松の木は、くるっと回転させると……。


忍者が潜んでいました。
くるっと回転させる仕組みは、線路の切り替え用の回転部分を利用しています。


製作時間が終わる頃に空中を滑り降りる忍者が作りたくなった★くん。
試行錯誤の末、空中移動が成功しました。


忍者屋敷にはさまざまな隙間や穴に忍者が隠れています。


★くんとお父さんのふたりで
断面図を推理する問題にチャレンジしてもらいました。

ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー『女の子の忍者屋敷作り』

物作りが好きでたまらない小1のAちゃん。今回、何がしたいのかたずねると、
「忍者屋敷が作りたい」とのことでした。
Aちゃんには、屋敷の家部分にあたる基本の形の作り方を学んでもらいました。
の舞台に似た作り方ですが、今回は同じ高さの形を量産するため、
紙の折り方を工夫しました。

Aちゃんは工作慣れした子なので、基本の作り方をどんどん発展させて
自分なりの世界を広げていました。
形を作り出す折り方に強い関心を寄せて、
「同じサイズの長方形2枚を重ねて、3対1くらいの比率で折ってから
一方をひっくり返して貼りあわせると長方形の筒の形になること」や、
同じサイズの左右対称な台形4枚を貼り合わせるとお城の石垣の形になること」などに
心から感動していました。

(↑写真の右上に小さく映っているのが、長方形2枚をひっくり返したときの様子です)
感動したときのAちゃんの口癖は、
「すごい!すごい!家に帰ってから、もう一回全部自分でやってみたい。もう一回、最初から全部自分で作りなおしてみたい」です。

Aちゃんの畳はタイル風でした。

スパンコールのカギと星で忍者の武器ができました。

算数が得意なAちゃんは、最レベ1年生の問題は、最後の算術特訓の問題以外は、
最高レベルのものもすべて簡単だったという話でした。
でも、算術特訓にあった集合の問題では混乱しているようでした。
そこで、「16人子どもがいる」という前提を頭に入れたうえで、
えんぴつをもらった14人の子を白丸でかきだし、
えんぴつもけしごむも両方もらった10人の子を黒丸でかきだしでから、
「14+10=24 子どもは全部で24人であっているかな?」とたずねました。
「それはおかしい!だって、子どもは全部で16人。」
「そうよね。ねこが好きな人?ってたずねて、Aちゃんが手をあげて、犬が好きな人?ってたずねてもAちゃんが手をあげたら、
1,2、2人だなってカウントすると変よね」
そんな話をしながら
どんな風にこの問題を整理したら正しい答えが出るのか、
いろいろ試してみながら話しあいました。
Aちゃんは集合の問題に興味がわいたようです。しっかり理解して解いていました。

「三角形の3つの角を切り取ってあわせると180度になる」ことを利用した手品を披露して遊んでいたら、
Aちゃんが四角形で試したがりました。
Aちゃんの予測は、「丸になる(360度のことのようです)」そうです。
正解。
わたしが「、四角形の4つの角をたすと、360度になるのよ。」と話すと、
Aちゃんは傍らにあった電卓に何かを打ち込んでから、「やっぱり、360度になった!」とうれしそうな声をあげました。
「360度というのは、三角形の3つの角の合計の180度を2回たしたものじゃないか」と
思ったそうなのです。
確かに折り紙で見ると、半分までの円にあたる形が180度なら
丸いかたちが360度だというなら、それをふたつたすと360度になるんじゃないか」と予測するのもわかります。
Aちゃんは物作りを通して、実際目にしているものを使って
さまざまな視点から物を考える習慣が身についている子です。