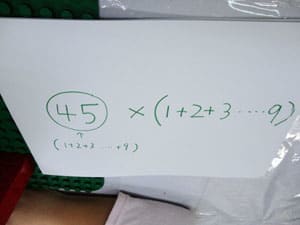１年間、たくさんの方々にご訪問いただき
本当にありがとうございました。
お正月のお休みは三が日だけなのですが、
これまでなかなか時間が取れなくて書けなかった
発達に凹凸がある子たちやＬＤのある子たちへの
学習のサポートの仕方をまとめていきたいと思っています。
ブロック講座には、広汎性発達障害等が原因で
学校での学習につまずいている子たちがかなり来てくれました。
ひとりひとりの子をもう少していねいに見てあげたかったのですが
時間に限りがありますからそういうわけにもいかず……。
ただ実際、子どもと会ってみてわたしなりにわかったことや
気づいたこともたくさんありました。
親御さんがどのようにそうした子をサポートしたらよいのか
戸惑っている理由や解決法についても
ぼんやりとしたものながらつかめました。
正月休みといっても３日だけなのですが、
何とか言葉にしていこうと考えています。
年末の大掃除は……かなり適当に……ぼちぼち進んでいます。
今年は３０日の夕方まで教室をしていたので、
大晦日の今になって即席の大掃除やら買い出しやらでバタバタしています。
掃除の合間の気晴らしにブログを書いています～♪
国語の学習につまずきがある子に教える時に気をつけていること ① の続きです。
国語でつまずいています……という子の学習をみていると、
「できない」という状態にしても、
「できない」という理由にしても、
「できるようになる」ためにしたらいいと思われる練習にしても、
実にさまざまです。
親御さんから、「国語の読解問題が苦手です。解けません。」というご相談をいただいて、
子どもに読解問題を解いてもらうと、
文字を読むので精一杯で、
何が書かれているのか理解しながら読むことができていないケースがあります。
そうした子は、文字を塊として読むことができなくて、区切る場所を間違っているのか、
漢字が読めないのか、ひらがなを読み間違えるのか、目の動かし方がたどたどしくて、読んでいる最中に別の行にずれてしまうのか、
読めるには読めるけど意味を理解しようという気に乏しいのか、
その子の状態を正確に把握することが大事です。
また、読みの問題とは異なるとはいえ読解ができない原因につながる
「いやなことはやりたくない」と言い張って意地でも読もうとしない、
学習と聞いただけでパニックを起こして大騒ぎになる、
すぐに「疲れた」といって寝転がったり、どこかへ行ってしまう、といった子も
何が問題か、見極める必要があると思います。
「読みながら理解する」ことができていない場合、
２、３行読むたびに
「何が書いてあったかな？」
「誰がでてきたの？」
「何をしたのかな？」
「それって書いてあるね。何のことだろう？ちょっと前に戻って探してみよう。」
「おてがみ出してきたよ、ってだれかがしゃべった言葉だね。かっこがあるから。
誰が言ったのかな？」など、たずねていると、
次第に意味を頭に入れながら読むようになってきます。
こうした練習に適しているのが、公文式の小学ドリル（本屋さんに売っています）
の学年ごとの「文章の読解」シリーズです。
数行だけ抜き出した問題に、
少しだけ質問がついています。
学習が困難な子でもできるレベルです。
読解力にかなり問題があった子も
学年相当のドリルを半分ほどやり遂げるころには
たいてい国語のテストに苦手はなくなっています。
次回に続きます。
ブロック講座の算数タイムで、
手で針を動かせる時計（１００円グッズ）で遊んでいた時のことです。
「長い針はどっちかな？大人みたいなの。長い長いやつ。どっちかな？」と
長針を選ばせて、「長い針」を学習していることを意識させてから、
学びはじめます。
（どっちが長い針で、どっちが短い針なのか
選ぶだけのことでも、教える相手が自閉症スペクトラムの知的な問題も少し抱えている子だったり、
多動気味で注意力の維持が難しい子だったりする
場合には、いちいち指で触れさせて、感触でも確かめながら
学習を進めるようにします。理解力や注意力が高まります。）
長針を５分の位置に合わせて
「何分かな？」とたずねると、
時計盤の１の数字にだまされて、「１分！」「１分！」と答える子どもたち。
この日、ブロック講座に集まっていた子らは４歳以上のしっかりしている子ばかり
だったのですが、
まだ時計の読み方は知りませんでした。
すぐさま、ルールを理解して
笑いながら学んだ子どもたち。
その後で、長針について学ぶ遊びをもうひとつ。
「時計の目盛をひとつずつ、１歳、２歳って数えていったら、
みんなの年だと、今、どこにいるのかな？」と問いかけます。
「ここ、ここ！」と
４や５や６のあたりを指す子ら。
「だったら、お父さんは？
おばあちゃんはどこだろう？」
時計盤の目盛の中で子どもたちの年齢を確かめると、
親御さんたちが「もうすぐ幼稚園だから」「もうすぐ学校なのに」と気をもんでいる子らも
まだ生まれてからこんなに少ししか日が経っていないんだな、と実感します。
この日、参加していた６歳の★くんは、大のひいおばあちゃん子。
この頃覚えた将棋の相手をこの９０代のひいおばあちゃんにしてもらっているそうです。
それがいい勝負で、お互いに楽しくて仕方がないようです。
時計盤で★くんのひいおばあちゃんの年を探そうと年齢をたずねると、
「９８歳（もしかして９２歳だったかも）」とのこと。
長い針が一回りして、６０分を過ぎても、
まだまだひいおばあちゃんの年には到達しませんでした。
子どもたちの間から、感動したようなため息が漏れていました。
今年最後のレッスンです。
（午前にブロック講座の様子はまた時間がある時に書きますね。）
小学３年生の算数クラブの女の子たちととても楽しい時間を過ごしました。
★ちゃんが持ってきてくれた『整数なぞぺー』
についていたという約数で遊ぶカードゲームをしました。
（さっそく教室用にも作らせていただきました）
場に出ている数の約数があれば出し、なければパス。
他の人がみんな出すカードがなければ、新しい数を場に出すことができます。
そうしてバトルしていって先にカードがなくなった人が勝ちです。
約数を素数の積であらわしている理由や、素数の積から約数を見つけ出す方法が
わかるようになりますね。とても魅力的なゲームです。
ミニチュアのケーキを作る手芸を楽しんだ後で、算数タイム。
ほんの一瞬で崩壊した九九タワーの記事で出していた問題、
「内部が空洞でなく、ぎっしりブロックが詰まっているとすると、
ブロックの個数はわかりますか？」
という問題を出してみました。
そこにいらした親御さんが、「中高生なら解けるかもしれないけど、
小学生だと難しいんじゃないですか？」とおっしゃっていました。
ところが、上の写真のような一部分だけをブロックで作ったものを見せながら
子どもたちに質問すると、「難しいのでは？」とおっしゃっていたお家のお子さんが
ねばり強く試行錯誤を続けて、
式まで出して正解し、他の子らも次々、「わかったわかった」と答えを出していきました。
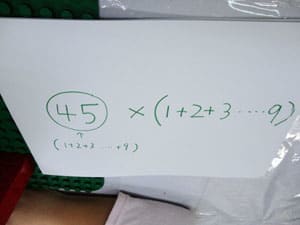
子どもたちが考えた式と答えは、
４５×（１＋２＋３＋４＋５＋６＋７＋８＋９）＝
４５×４５＝２０２５
一番手前の赤いブロックの塊が１から９までの足し算が
１たす９、２たす８……と組み合わせて、４５と即答できるので、
その後ろの列が４５の２つ分、その後ろが４５の３つ分……となるため、
九九タワーに必要な総数は４５×４５となるのです。
それにしても、子どもたちの間から正しい解き方が出てくるとは
思わなかったので、その成長ぶりにびっくりしました。
もうひとつ、「みんな、算数のセンスが伸びてきたな～」と感心したのが
次の問題。
発達に凹凸のある小１の★くん、小２の☆くんのレッスンです。
ふたりとも国語の読解問題につまずきがみられるというお話をうかがって、
『トップクラス問題集の２年生』と『ちょっと難しい１０００のことば』というテキストを使って
国語の学習をしました。（★くんは１年生でさまざまな面で困り感を抱えている子ですが、
知力が高いので、☆くんと同じ
２年生のワークで学んでいます）
学習の様子は後でするとして、まず今回、ふたりが作っていた工作とブロックの作品を
紹介しますね。
上の作品は☆くん作の駅の自動改札の機械です。
一方からカードを投入すると、ちゃんともう一方から出てくるようになっています。
病院の検査で空間認知力の弱さを指摘されていた★くんですが、
工作が好きになるにつれて、立体や図形を扱う問題がとても得意になってきました。
教室に着くなり、「工作がしたいから空き箱はないの？」とたずねます。
ティッシュの空き箱を入れている袋を渡すと、
あっという間に５つの箱をテープでつないで、かなり大きな自動改札機を作っていました。
（すごいティッシュの空き箱の消費量！）
数ヶ月前から★くんと☆くんのブームは自動販売機やがちゃぽんなどの内部の仕組みを
作ることなのです。
★くんは、サランラップの芯に長い紙を巻きつけて、動かす仕掛けを作ることにしました。
ちゃんとカードが出てきて大満足♪
大きなホッケー風のゲームも作って遊びました。
☆くんは、一度教室で作って以来はまっている
自動販売機作りをブロックでしていました。
押し出す仕組みで、商品が出てきます。
商品を出す時、取り出し口に手を入れなくてはならないので、ちょっと難ありなのですが、
本人は自分の作品に大満足のようでした。
それでは、記事のタイトルでもある国語の学習について
書きますね。
『ちょっと難しい１０００のことば』という本は
語彙が少なかったり、自分流の言葉の使い方が多くて、耳にした言葉から類推して
「だいたいこういう意味じゃないかな？」とピンとくることがあまりない子の学習にとても役立ちます。
毎ページ５問ずつの線つなぎのクイズのように
楽しく取り組めるようになっています。
①いんぼうをたくらむ
②お母さんが先生にめんかいする。
③いちかばちかやってみよう。
といった聞いたことがありそうで、どういう意味かわかりにくいことばを、
短い解答と結び付けていきます。
Ａ 人と会うこと。
Ｂ うまくいくか失敗するかわからないが。
Ｃ よくないことを計画すること。
★くんにこうした問題を出したところ、どれも正解することができました。
それほど言葉を知っているわけではないのでしょうが、類推するのが上手な
勘のいい子なので、五択になっている問題だと、「どれが答えに近そうか」がピンときたようです。
ただ、★くんがこの問題を解く姿を見て、文字を読む力のたどたどしさが
気にかかりました。
読み間違いや読み飛ばしが多く、たった二行の短い文でも
自分の読む力の危うさが原因で、何が書いてあったのか記憶に残っていないようでもありました。
今回の学習では、読みでつまずきかけるたびに、少し読み方のフォローをしていたので、
自分ひとりで読んで問題をすると、とたんにできる問題が減るようにも感じました。
理解力や考える力は高い子なので、
文字を読む際のつまずきを無くしていってあげれば、
今、国語でつまずいている状態から脱することができるのかもしれません。
次回に続きます。
「いつもミニカーでばかり遊んでいて、遊びが発展しません」
「いつもお人形ごっこばかりしていて、別の遊びをしたがりません」
なんて相談をよくお受けします。
何度やっても飽きないほど好きな遊びがあるなら、その遊びを思う存分させてあげると
いいと思います。
そうしたいつもと同じ遊びのなかで、数学的なセンスを育む働きかけ
を紹介します。
コツ１ ＜できあがったおもちゃをそろえすぎず、
積み木やブロックで小道具を作る＞
最初は大人が作ってあげます。
車なら車庫、お風呂（車が入ります）、道路など……。
人形なら椅子、テーブル、お風呂など……。
空間認知能力が伸びるだけでなく、イメージする力がついてきます。
算数の図形分野の力がはぐくまれます。
コツ２ ＜困った場面に遭遇させて、
サイズや量への気づきをうながす＞
子どもは最初、大きさについてでたらめな感性を持っています。
教えずぎず、たくさん失敗させて、
「あれ、小さすぎる」「あれ、あふれちゃう」といった体験をたくさんさせます。
コツ３ ＜「こんなものがほしい」「こうしたい」と思ったら、頭と手を使って解決する習慣を＞
「こんなものがほしい」「こうしたい」と思ったとき、
自分の頭をひねって考えると、必ず良い解決法があるんだ、と実感する
体験をたくさんさせてあげます。
工作も、工作の時間にさせるものではなく、
日常の一こまやいつもの遊びのなかで、
「こうだったらいいな」と実現するツールとして体験させてあげたいです。
ブロックや積み木や紙を使って
問題を解決することは、
数学的なセンスを育むのにとても役立ちます。
今回のブロック講座には、年中さんの●くん、年長さんの○ちゃん、７歳の☆くん、★ちゃんが
参加してくれました。
風邪が流行中のため、毎回、１人はお休みがあるので残念です。
何を作りたいのかの話合いでは、全員一致で「ロボット！」とのこと。
写真は首や腕などが動くロボットです。○ちゃんとわたしがいっしょに作った作品です。
背後から見た動く仕掛けです。首の回転には、線路の切り替え用のパーツを使用しています。
最初に子どもたちに学んでもらった甲殻類のロボットの作り方。
子どもたちはそうした基本を応用させて
さまざまなロボットを作っていきました。
クラゲ型ロボット
へび型ロボット製作中。
●くんが作った戦闘機。
☆くん作、エビ型ロボット？
みんなで協力して、モノレールなど、他にもいろんなものを作りました。
ブロック講座では、毎回ブロックで動く仕組みや知育玩具を作る方法を学ぶ時間や
参加する子の年齢に合わせた算数タイムも設けているのですが、
（年末でバタバタしていますので……）その様子は
年明けにでも書かせていただきますね。
午前の部の子たちの作品を午後の部の子に残しておいてあげたら、
「わぁ～！」と感嘆の声があがりました。
何を作りたいか話しあっていたら、７歳の☆ちゃんと５歳の●ちゃんは、
「２階や３階があって、お風呂とか、動物を飼うところとかがあるお家」
「プールにお魚とかがいるところもあって、クリスマスのリースとかも作りたい」という
話でした。
午前の部の子のお寺や鉄道博物館がとても立派だったので、壊すのが惜しくて、
作品の一部をリサイクルさせていただいて、豪華なお家を作ってみてはどうか、と提案しました。
お寺はこんな風に改装されて、ライトも灯りました。
お部屋の奥には、別の部屋に通じる通路もできています。
おそらく億万長者が暮らす豪邸なんでしょうね。
エレベーターでプラネタリウムを備えた屋上庭園に行くことができます。
動物ショーができるペンギンやあしかを飼っている巨大プールまでも。
飛行機を作っていた１０歳の●くん。
デコレーションするアイデアが卓越しています。
だんだん立派になっていく飛行機は次第にノアの箱舟のように
なっていました。
７歳の◎くんは線路や電車を作った後で、ドリンクバーが備えられている
サービスのいい駅を作っていました。
黄色い線は、列車の到着時にそれより後ろに下がるための線です。
ブロック作品を作る姿から、
●くんは空間認知力がとても高い子のようだったので、
左のような中学入試問題にチャレンジしてもらいました。
正面と横から見た図と、真上から見た図から、
体積の最大と最小の場合を求めます。
●くんはどちらもしっかり解けていました。
７歳の★くんの作品。名古屋の『鉄道博物館』なのだそうです。
名古屋の……と前置きする★くんですが、
関西の子のためか、なぜか海遊館を思わせる外観に……。
それにしても、本当に行ってみたくなるようなすてきな博物館ができていますね。
★くんの横では、同じ７歳の●くんがお寺作りにチャレンジしていました。
色にも形にも凝って黙々と作っていきます。
熱心に作りながらも、弟の☆くんがブロックのパーツを探しにくるたびに、
サッと、必要なパーツを探してあげる優しいお兄ちゃんの一面も見せていました。
立派なお寺ですね。
４歳の○くんと３歳の☆くんは
「お魚釣りの釣るやつと船を作りたい」と言って
がんばっていたのですが、船は途中で釣り場になりました。
実はブロック講座には大事な「おきて」があります。
ブロック講座なので、ブロック以外のおもちゃに触って遊んではいけない、という
ルールです。
この「おきて」を破った子には、
「必ず、触ってしまったおもちゃをブロックで作らなくてはならない」というバツが
あります。
これまで、この「おきて」を破る子はほとんどなかったのですが、
今回、○くんと☆くんが繰り返しルール違反をしたため、
「触ったおもちゃの作り方をわたしに習って、作る」はめに陥っていました。
ふたりが繰り返し触っていたおもちゃのひとつは、ユーフォーキャッチャーです。
ユーフォーキャッチャーのレバーで動かす部分を再現して
左右に動く釣りざおを作ってもらいました。
電車のおもちゃも何度も触ったため、何個も電車を作ることになり、
罰則で作った電車を★くんの鉄道博物館に寄贈することになりました。
↓
この日参加してくれていた４歳の◎くんはすてきな電車の駅を作っていたのですが、
写真が残っておらず残念でした。
