日高敏隆氏の『生きものの流儀』という著書に興味深い話が載っていました。
簡単に要約して紹介しますね。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
著者が当時の成城学園小学校の先生だった庄司和晃先生からうかがった話です。
ある日、庄司先生は子どもたちに画用紙を配って「さあ、アリの絵を描いてください」と
言ったそうです。たちまちイメージできたらしい子もいれば、まだイメージをさぐっている子もいたそうです。
できた絵を見ると、アリの身体は頭と胴体のふたつに分かれていて、
人間がイメージしている「動物」の姿であって、
たいていの女の子はそのアリにリボンまでつけていたのだとか。
次に庄司先生は、子どもたちひとりに1匹ずつ、「実物」のアリを渡して、
「これがほんもののアリだよ。今度はそれをようく見て、アリの絵を描いてください。」と言ったそうです。
すると、驚いたことに、実物のアリを見て描いたはずの絵でも、その多くは
依然としてアリは胴と頭、足は四本だったのだとか。
著者はそこに人間のイリュージョンというものの見たような気がしたということです。
どの子も実物はちゃんとまじめに見ているはずなのに、
実物が自分の思っているように見えてしまい、それ以外のものは、
存在しなくなっているのです。
庄司先生は、その後、
「……よく描けてきたなあ。えらい、えらい。だけど、アリの体って
ほんとに頭と胴体しかないのかい?」とか、「じゃぁ、その六本の足はどこに生えている?」といった
会話を通した指導をして、もう一枚、子どもたちに絵を描かせると、
子どもたちの絵はより正確なものになりました。(が、依然、赤いリボンをつけている子らはいたようですが)
「イリュージョンが修正されるには、これだけの手間が必要なのだ。しかも現実の生きたアリが
手もとにいるのにである」と著者は人間の持っている錯覚や幻想のもつ意味と力が
少し理解できるようになったと述べています。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
先に紹介した話で面白かったのは、
実物を見た後で、最初の動物もどきのアリの絵から、
頭、胸、腹、そして6本の肢という昆虫の姿に変化させることができた子というのは、
一枚目の絵を何度も描いたり消したりしていた子どもの場合に
多かったという著者の発見です。
何でも、一枚目の絵を太い鉛筆で自信満々、頭と胴、四本の肢と描いた子の絵は、
実物を見ても何一つ変わっていなかったそうです。
この話を読んだ数日後の小学2年生の女の子ふたりのレッスンで
こんな気になる出来事がありました。
この2年生の子たちは、もともと観察力があって、思考力も高い子たち
です。
そのうちの子のひとりは、2年生になったあたりから、長文を読んで理解する力が伸びて、
中学入試向けの和差算や植木算や旅人算なども
ひねった問題でもテキパキと解けるようになってきました。
それでこれまでは虹色教室で月に1回、そうした問題に触れる程度だったのですが、
お家でも最レベの最高レベルの問題を中心に予習をしてくるようになりました。
わたしはこの子がやる気と自信に満ちて学習に取り組むようになった
こと自体はうれしくて、その意欲を大事に育んでいこうと感じた反面、
ちょっと気になる態度に引っかかるようになってきました。
お家で学んでくる際に、正しい式を教わってくるようになったためか、
問題を見たとたん、複雑なものでも数字を操作して、
正しい公式で解こうとする姿が目立つようになったのです。
でも、少し前なら、紙に絵図を描いてみて、考えこみながら解いていたのが、
問題を見たとたん、数を正しい公式にあてはめるようにさらさら
解くようにもなっていたのです。
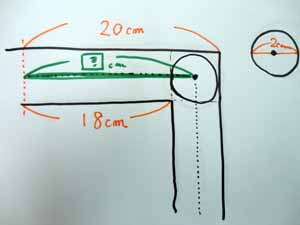
そこで、その子がお家ではしていない3年生の最レベの問題から、
一部を取り出して、上の写真の図を描いて、緑色の線の部分、
直径2センチの円の中心が描く線について、
長さをたずねたところ、「18センチ?ん、20センチかな?」とでたらめなことを言いました。
何度もよく見るようにうながしても、緑の線が18センチの線より長いということや、
20センチよりも短いということに気づけません。
この子は、本来、とても観察力があって、直観がよく働く子ですから、
この線の違いに気づかないわけはないのです。
でも、「小学3年生のだと難しいに違いない」とか「やったことがない問題は解けないに違いない」とか
「算数の問題は、そこにあるどれかの数字を言えばいいはず」といった思い込みが邪魔をするのか、
素直に絵が見れなくなっていました。
難しい問題をさらさらと正しい式を立てて解けるようになると、
周囲から「すごい~」という賞賛を浴びることが多くなります。
すると、子どもはうれしくて、がんばる意欲を見せるときがあるのですが、
その時期の周囲の大人のフォローやサポートが
とても重要だと思っています。
「すごい~」と言われることにばかり心が奪われると、
絵図を描いて、試行錯誤して、自己流の間違った式を立てるより、
「最初から答えを見て、暗記してしまえばいいじゃん」という態度に傾き
がちになるからです。
そうした時に陥りやすいのは、
意味を理解せずに、
「こういう言葉が出てくるこういう問い方の時は、
この数からこの数を引いて、それにこの数をかければいいんだった」といった
わからないままに丸飲みするように解く癖がつくことです。
そういう癖がつきはじめている時の危険信号は、
現物を見ているのに、
自分のなかのイリュージョンに自信を持つあまりに、
現物を正しく見ることができなくなっているという状態だと
感じています。
線が長いか短いか、
素直に見るならすぐにわかるのに、
「前にどんな解き方だったかな?」と
記憶をさぐる作業に忙しくて、目の前のものが見れなくなる場合があるのです。
もちろん、意欲的に学習し、長い文を理解して解く力が伸びること自体はいいことで、
それを認めて、褒めて、大事にしてあげなくてはなりません。
でも、その時に、
子どもが問題を自分で具体物を操作して説明できるほどわかっておらず、
自分で絵図をきちんと描いて、自分の間違いを修正できるほど成長していないにも関わらず、
式さえ暗記すれば、そちらが正しい答えなんだよ……と教えこんでしまうことは
危険なことだと思うのです。
正しい式を覚えるのは、
まず問題の意味が正確にわかって、自分で自在に操作できるようになってからで十分で、
わかりもしないのに、正しい式だけかけるようになると、
自分がわかっていると錯覚して、さっぱり応用のきかない力をつけてしまうからです。
前回の記事にe-com子育ての羊先生から次のようなコメントをいただきました。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
ヒトの五感というのは脳で処理をする過程で、
記憶や経験に影響されるというのを聞いたことがあります。
アリの絵の話は、ヒトが見たいものを見るという例ですね。
実はまだブログでアップしていない記事で、公式をわすれたから解けないという
生徒の話を書きました。公式から離れて考えれば持てる知識で解けるのにです。
「正しい解法」という枠に囚われている生徒が多いように感じます。
その原因を作っているのは大人なのですね。
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
羊先生のブログで、
という記事を読んでとても共感しました。
京都産業大学の永田和宏教授の
「今の若い人は、現実の世界から何かを引き出すという訓練を全く受けていませんね。」
という指摘からはじまる考えさせる文章や
JT生命誌研究館館長 中村桂子氏の
「 教育や学問では一人一人の状況に応じて対象から引き出すものが違ってくるところが大事なのに、
どんな子供も同じことから同じものを引き出すように仕向けている風潮がありますね」
というこちらも現在の教育問題の急所を突く指摘と取り上げて、
羊先生がわかりやすく解説してくださっています。
ぜひ、ブログに遊びにいってくださいね。
前回の記事で、教室の子が意欲的に学習に取り組むようになると同時に
目の前の事実が素直に眺められなくなる事態が起こったという話を書きました。
「デジタルからデジタルへ」情報を変換することを覚えるほど、
目の前の現実の世界や自分が向き合っている対象を正しく読み説いて、
そこから価値ある何かを生み出していくことは難しくなりがちです。
でも、だからといってプリントや本で学んだり、
その子の能力を超える概念に
触れたりすることが悪いわけではないはずです。
羊先生がおっしゃる通り、「正しい解法という枠に囚われるあまり、
公式を忘れると解けなくなるような原因を作る」 大人の態度に
問題があるのではないでしょうか。



















