
『かけ算には順序があるのか』 高橋誠/岩波科学ライブラリー
■ 本書のタイトルを見て、順序なんてないって思ったのですが、どうもそうではなさそうで・・・。
小学校の算数で「6人に4個ずつミカンを配ると、何個必要ですか」という問題に、6×4=24という式を書くとバツにされるそうです。なぜでしょう。本書によると、教科書のかけ算の章の最初に、1つ分の数×いくつ分=ぜんぶの数という式が出てくるそうです。教科書によって表現は少しずつ違っているようですが。この問題では4×6=24という式が正解ということなんですね。
1個100円のパンを5個買うといくらですかという問題だと、100×5=500 つまり単価×数量=金額という順序の式でないとダメ、ということになります。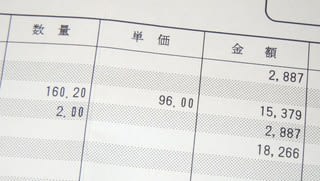
でも、でも・・・。手元にある請求書をみると、記載欄は数量、単価、金額の順序で並んでいます。これが一般的な並び順のようです。これは一体どういうことなんでしょう。
先の問題については大阪府の小学校で親と学校との間で論争になったことがあったそうで**式は思考の過程を表わすもので、答えさえあえばどちらでもいいというわけにはいかない。こどもの発達段階からみて、この場合、4×6と指導するのが最善の方法だ。**という学校のコメントが紹介されています。(13頁)
ネコが6ひきいれば、足は全部でいくつですか、というような問題であれば、私はまずネコの全身が浮かび、それから足にズームインします。ですから、状況把握のプロセス(というほどのものでもありませんが)を式にするなら6×4となります。きっと小学生にも同じ捉え方をする子がいると思います。でも小学校ではこの式ではバツなんですね。
このような問題は「1つ分の数×いくつ分=ぜんぶの数」でも「いくつ分×1つ分の数=ぜんぶの数」でもどっちでもいいと思います。
同じ答えを「同じ考え方」で求めるように指導する方が楽、指導しやすいでしょう。どうも教える側の都合が優先されているような気がします。子どもたち一人ひとりを相手にする必要がありませんから。でもいろんな考え方があって当然で、そのことを認めた上で子どもたち一人ひとりと向き合って指導して欲しいのもだと思います。









