どう考えても、その視点から見ても、三角で、四角にならないのでは?というメールが有りましたので補足説明です。
7つめの四角を考えるに、図形を立体化して見る必要は確かにあります。
表面的に見るだけなら、紫の△底辺の2辺が角度をなしているとすれば、 前の台形図が単なる線に見える角度まで目線を落としていかないと、御指摘通りに、この二辺は直線に見えるようにはなりません。
ただ、全ての線が全く重なりのない、立体という概念で見なければならない!とは設問に書いてはいない。 大体にしてそれやると6個の四角もそれぞれ重なって解答にはならないはずです。
出題図そのものを、どう解釈するか?で起きる事というのが有ります。
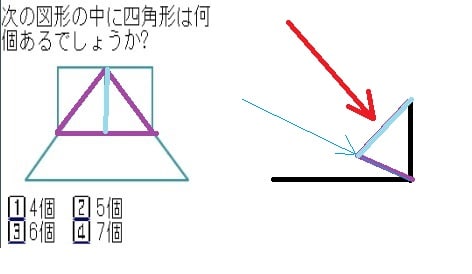
下の図、右側は7つめの四角を導きだした根拠で、横から見た物なのですが、設問の図面における視点角度は細い水色矢印の方向からで、この角度から見ると2辺は直線に見えます。
3角に見える四角の底辺が、単に一番下の台形図面の一辺と丁度重なっているなら、赤矢印の視点を頭に置いて見れば四角がそこにある訳です。
もし設問図の中に、影でも書かれてたりでもしたら3次元的立体図で有る事は誰にでも解ってしまい、これまた誰にでも回答可能な問題となってしまうわけでして、それではIQを測る設問としてはまったくもって不適。
出題者は、回答者が出題者の隠した意図(遠近法を取り込んである一部立体)まで読み込んで回答する事を予測した、想像力の範疇まで考慮して問題を造っている、
と考えるのが正しいわけです。
まとめると、図形を二次元図として見ようが三次元図として見ようが一向に構わず、四角が有れば良いわけですが。
以上補足でした。