レ・クリント風プリーツ球体照明（１）：設計の準備

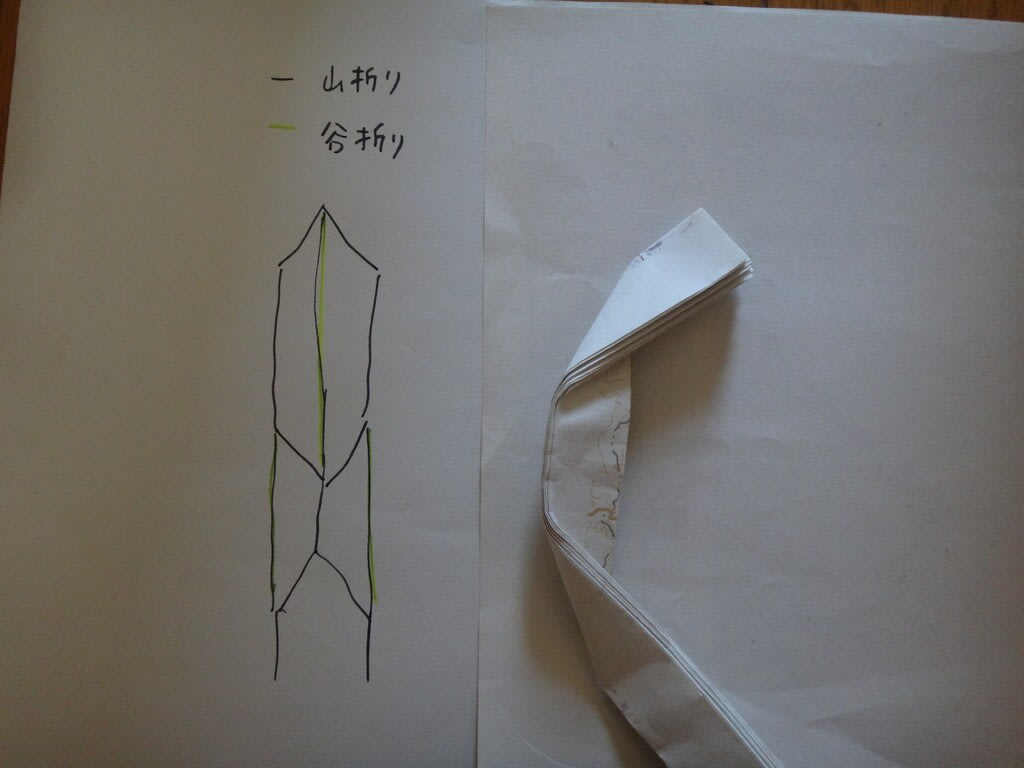
2019年１月頃、ル・クリントのランプシェードにインスパイアされて、こんな照明カバーを作りました。
（写真は、2020年4月に微調整して場所移動したときに撮影）

で、このとき使ったプラスチック障子紙、何故か２枚入りを買ったので、１枚で足りて、１枚余っていました。

これを有効利用したいものです。 もうひとつ、作ろう。 今度は、お店で見たこれを作ってみたい・・・。

紙を折って、球体ができるなんて、不思議です。 前は、適当に自己流で作りましたが、今度はなるべく同じものを作りたいです。 どういう設計になっているのだろうか。 じーっと観察してみると・・・

左側が前に自作したもの。右が今回作りたい球体。 ヒダヒダの形状というか、構成する多角形の形が異なります。 左は縦の線が、山になったり谷になったりしているし、縦に細長い６角形で構成されています。 右は縦の線がすべて谷折り。そして菱形で構成されています。 図にするとこんな感じ。

左が前につくったもの、右がこれから作りたい球体。 右は、菱形で構成されています。 実際に紙を折ってみながら確認すると・・・

こういう折り方でつくると、表面が六角形になってきます。

こういう折り方だと、菱形で構成されることになります。 こうやって屏風畳みの紙を、斜め線が連続するようにに何度か折って、半円をつくるようにする、ということ。 適当に折ってみて思ったのですが、作りたいサイズと、屏風畳みの幅は関係しているような気がします。 適当な幅の屏風畳みを適当に折ったのでは、丸くなっていかないような・・・。 （前に作った時は、適当な幅の屏風畳みを適当に折っただけだった・・・・） で、うまいこと説明できませんが、正多角形を作るためには、次のような法則があることが分かりました。

例えば、投影したときに正10角形になるようなボールを作るには、 ・屏風畳みの幅は、蛍光イエローの部分 ・紙の長さに相当するのは、頂点を一個飛ばしにした部分の長さ、つまり蛍光ピンクの部分の長さ となります。

直角三角形の各辺の長さは、こういう計算です（グーグル先生、ありがとう！）。 半径ｒの正2n角形にしたい場合、 中心角θ＝360/2ｎ 紙の縦の長さ＝r・sinθ ｘ n 屏風畳みの幅＝ｒ－ｒ・cosθ 紙の横幅＝ヒダの角度60度とすると円周の約２倍＝２×２πｒ 実際にやってみます。 （うっとおしかったら数式の部分は飛ばしちゃって、写真だけ見て下さいませ） ■正６角形の場合 半径10ｃｍの正６角形とすると θ＝360/6　＝60 紙の縦の長さ＝10・sin60° ｘ 3 　　　　　　＝10・0.87 ｘ 3 　　　　　　≒26.0 屏風畳みの幅＝ｒ－ｒ・cosθ 　　　　　　＝10－10・0.5 　　　　　　＝5

26cmの長さ（×横幅約125cmもしくはもっと）の紙を、5cm幅に折り畳み、26cmが３区分になるように斜め線を入れて菱形を作って畳むと、投影形状が６角形のボールになります。 （ヒダが粗くてボールとは呼べないかもしれませんが） （写真はテストピースなので横幅30cm程度でつくっています） ■正８角形の場合 半径10ｃｍの正８角形の場合 θ＝360/8　＝45°  紙の縦の長さ＝10・sin45° ｘ 4 　　　　　　＝10・0.71 ｘ 4 　　　　　　≒28.4 屏風畳みの幅＝ｒ－ｒ・cosθ 　　　　　　＝10－10・0.707 　　　　　　＝2.9

28.4cmの長さ（×横幅約127.6cmもしくはもっと）の紙を、2.9cm幅に折り畳み、28.4cmが４区分になるように斜め線を入れて菱形を作って畳むと、投影形状が８角形のボールになります。 （写真はテストピースなので横幅30cm程度でつくっています） ■正10角形の場合 半径10ｃｍの正10角形の場合 θ＝360/10　＝36 紙の縦の長さ＝10・sin36° ｘ 5 　　　　　　＝10・0.59 ｘ 5 　　　　　　≒29.5 屏風畳みの幅＝ｒ－ｒ・cosθ 　　　　　　＝10－10・0.81 　　　　　　＝1.9

29.5cmの長さ（×横幅約125.4cmもしくはもっと）の紙を、1.9cm幅に折り畳み、29.5cmが5区分になるように斜め線を入れて菱形を作って畳むと、投影形状が10角形のボールになります。 （写真はテストピースなので横幅30cm程度でつくっています） だいぶボールぽくなってきました。 ■正12角形の場合 半径10ｃｍの正12角形の場合 θ＝360/12　＝30° 紙の縦の長さ＝10・sin30° ｘ 6 　　　　　　＝10・0.5 ｘ 6 　　　　　　＝30 屏風畳みの幅＝ｒ－ｒ・cosθ 　　　　　　＝10－10・0.866 　　　　　　＝1.34

30cmの長さ（×横幅約126cmもしくはもっと）の紙を、1.34cm幅に折り畳み、30cmが6区分になるように斜め線を入れて菱形を作って畳むと、投影形状が12角形のボールになります。 とてもヒダが浅くなってきました。 作りたい球体は、写真をじーっとにらんで数えてみると、最後の12角形だと思います。 半径25cm、直径50cmくらいでちょうど、照明器具を中にいれられるし、障子紙の縦の長さ90cmにおさまりそうです。

実物大投影モデル。

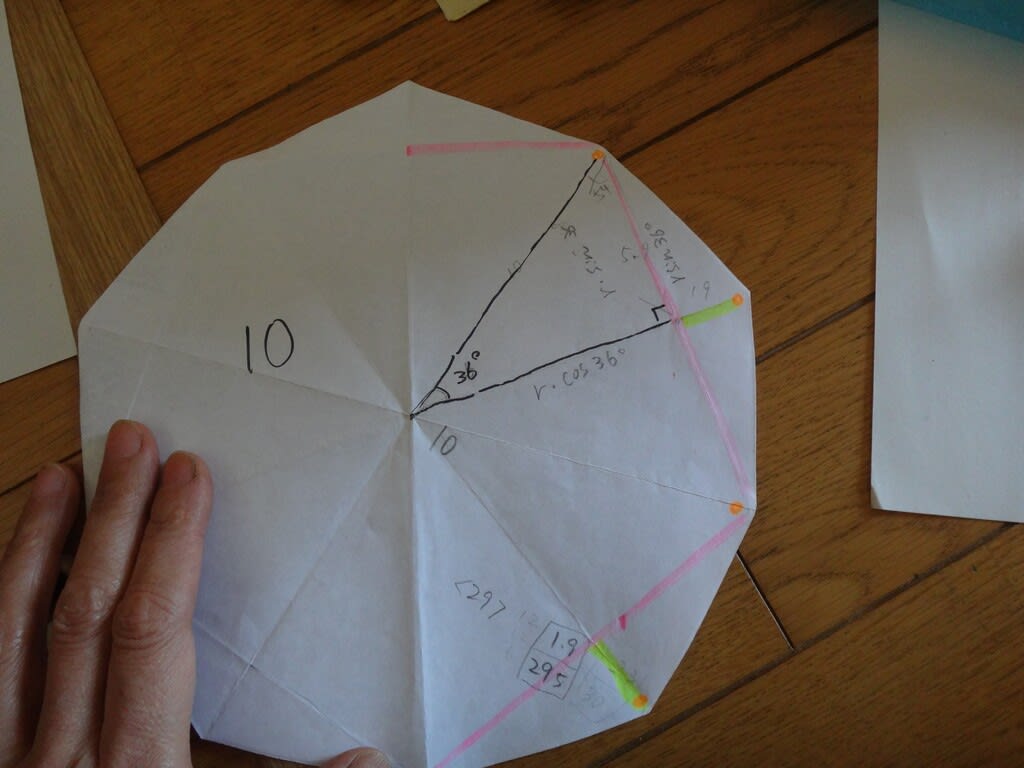
半径25ｃｍの正12角形の場合
θ＝360/12　＝30°
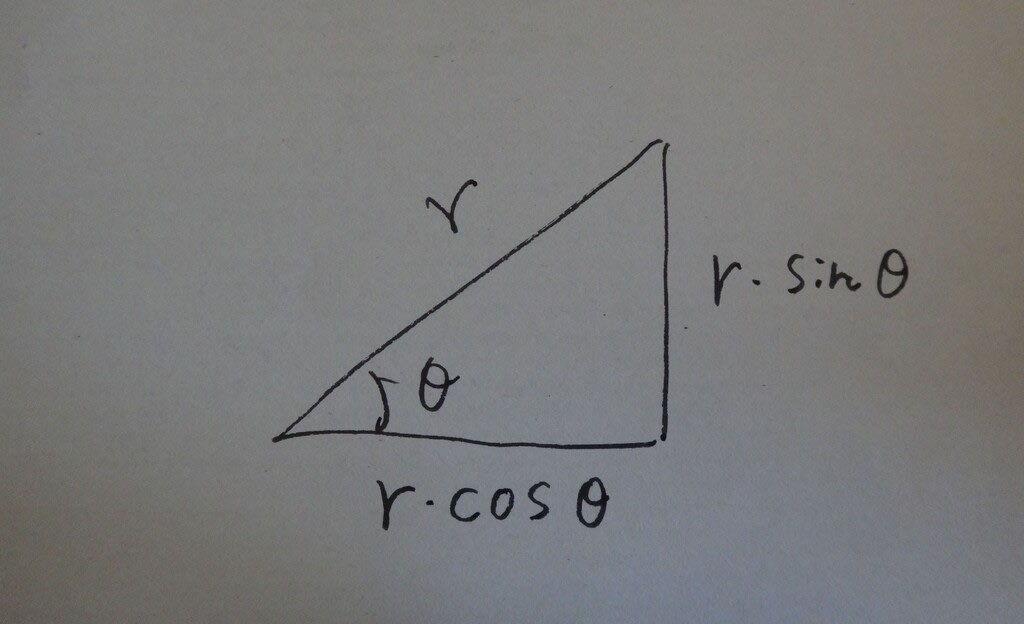
紙の縦の長さ＝25・sin30° ｘ 6
　　　　　　＝25・0.5 ｘ 6
　　　　　　＝75
屏風畳みの幅＝ｒ－ｒ・cosθ
　　　　　　＝25－25・0.866
　　　　　　＝3.35
紙の横幅＝２×２πｒ
　　　　＝２×２・3.14・25
　　　　＝314　　

紙の縦の長さは、90cmにおさまるし、ヒダの幅は、3.3cmでよさそう。
横幅は、計算上は障子紙180cmの２枚分（360cm）はなくてもよさそうですが、丁度２枚分加工することにします。
１枚買い足すことになります。


これにあうような感じで、まずは実物大サンプルを作っていきます。

（続く）